题目内容
【题目】阅读下列两则材料，回答问题：
材料一：我们将
与
称为一对“对偶式”因为
，所以构造“对俩式”相乘可以有效地将和中的
去掉.例如：已知
，求
的值．解：
，
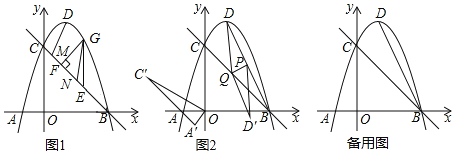
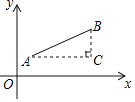
材料二：如图，点
，点
，以AB为斜边作
，则
，于是
，
，所以
.反之，可将代数式
的值看作点
到点
的距离.
例如：
=
．
所以可将代数式
的值看作点
到点
的距离．
利用材料一，解关于x的方程：
，其中
；
利用材料二，求代数式
的最小值，并求出此时y与x的函数关系式，写出x的取值范图；
将
所得的y与x的函数关系式和x的取值范围代入
中解出x，直接写出x的值．
【答案】（1）
；（2）①
，
；②
.
【解析】
根据理解材料一的内容进行解答，比对这题很容易解决．
中把根式下的式子转化成平方
平方的形式，转化成点到点的距离问题，根据两点之间距离最短，所以当三个点共线时距离最短，可以求出最小值和函数关系式
中也根据材料二的内容来解答求出x的值．
根据材料一；
,
，
，
,
,
解得：,
；
解：由材料二知：
，
，
可将
的值看作点
到点
的距离
的值看作点到点
的距离，
∴
，
当代数式取最小值，
即点与点，在同一条直线上，并且点位点
的中间，
的最小值
=
，
且
，
设过，，的直线解析式为：
，
解得：
，
；
中，
，
(ⅰ),
又
(ⅱ)
由(ⅰ)
得：
，
解得：
舍
，
，
的值为.
练习册系列答案
口算题天天练系列答案
相关题目
