题目内容
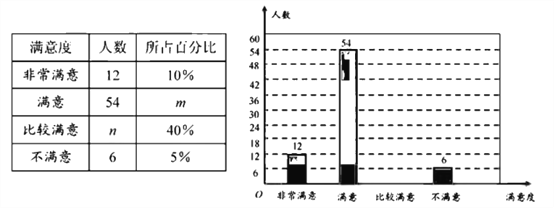
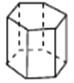
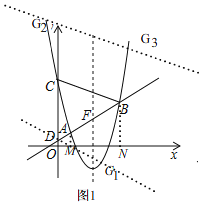
【题目】如图,在平面直角坐标系![]() 中,以直线
中,以直线![]() 为对称轴的抛物线
为对称轴的抛物线![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于
轴交于![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的函数表达式;
(2)设直线![]() 与抛物线的对称轴的交点为
与抛物线的对称轴的交点为![]() ,
,![]() 是抛物线上位于对称轴右侧的一点,若
是抛物线上位于对称轴右侧的一点,若![]() ,且
,且![]() 与
与![]() 的面积相等,求点
的面积相等,求点![]() 的坐标;
的坐标;
(3)若在![]() 轴上有且只有一点
轴上有且只有一点![]() ,使
,使![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() .;(2)点
.;(2)点![]() 坐标为
坐标为![]() ;
;![]() .(3)
.(3)![]() .
.
【解析】(1)根据已知列出方程组求解即可;
(2)作AM⊥x轴,BN⊥x轴,垂足分别为M,N,求出直线l的解析式,再分两种情况分别求出G点坐标即可;
(3)根据题意分析得出以AB为直径的圆与x轴只有一个交点,且P为切点,P为MN的中点,运用三角形相似建立等量关系列出方程求解即可.
(1)由题可得: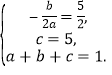 解得
解得![]() ,
,![]() ,
,![]() .
.
![]() 二次函数解析式为:
二次函数解析式为:![]() .
.
(2)作![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() ,则
,则![]() .
.
![]() ,
,![]() ,
,![]() ,
,
 ,解得
,解得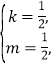 ,
,![]() ,
,![]() .
.
同理,![]() .
.
![]() ,
,
![]() ①
①![]() (
(![]() 在
在![]() 下方),
下方),![]() ,
,
![]() ,即
,即![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() .
.
②![]() 在
在![]() 上方时,直线
上方时,直线![]() 与
与![]() 关于
关于![]() 对称.
对称.
![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() .
.
综上所述,点![]() 坐标为
坐标为![]() ;
;![]() .
.
(3)由题意可得:![]() .
.
![]() ,
,![]() ,
,![]() ,即
,即![]() .
.
![]() ,
,![]() ,
,![]() .
.
设![]() 的中点为
的中点为![]() ,
,
![]() 点有且只有一个,
点有且只有一个,![]() 以
以![]() 为直径的圆与
为直径的圆与![]() 轴只有一个交点,且
轴只有一个交点,且![]() 为切点.
为切点.
![]() 轴,
轴,![]() 为
为![]() 的中点,
的中点,![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,![]() .
.
![]() ,
,![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目