Question

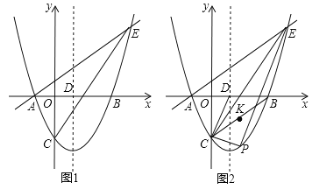
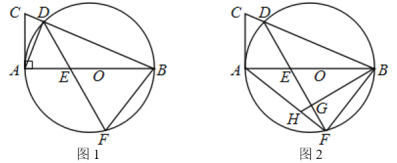
【题目】如图1，AB为⊙O的直径，AC与⊙O相切于点A，BC与⊙O交于点D，点F是直径AB下方半圆上一点（不与A，B重合），连接DF，交AB于点E，

（1）求证：∠C＝∠F；

（2）如图2，若DF＝DB，连接AF．

①求证：∠FAE＝2∠AFE；

②作BH⊥FD于点G，与AF交于点H．若AH＝2HF，CD＝1，求BG的长．

Answer 1

【答案】（1）见解析；（2）①见解析；②

【解析】

（1）利用等角的余角相等以及圆周角定理即可解决问题．
（2）①如图2中，连接DO，延长DO交BF于K．想办法证明AF∥DK，利用等腰三角形的性质证明∠FDB=2∠AFD即可解决问题．
②如图2中，设DK交BH于J，连接JF．首先证明四边形AFJD是平行四边形，推出，设GH=m，GJ=3m，则JH=JF=JB=4m，推出GF==m，由∠C=∠BFG，推出tanC=tan∠BFG===，求出AD即可解决问题．

解：（1）证明：如图1中，

∵AC是切线，
∴AB⊥AC，
∴∠CAB=90°，
∵AB是直径，
∴∠ADB=∠ADC=90°，
∵∠C+∠CAD=90°，∠CAD+∠DAB=90°，
∴∠C=∠DAB，
∵∠DAB=∠F，
∴∠C=∠F．

（2）①证明：如图2中，连接DO，延长DO交BF于K．

∵DF=DB，

∴，

∴DK⊥BF，
∴∠FDK=∠BDK，
∵AB是直径，
∴∠AFB=∠DKB=90°，
∴DK∥AF，
∴∠AFD=∠FDK，
∴∠FDB=2∠AFD，
∵∠EAF=∠FDB，
∴∠EAF=2∠BDF．

②解：如图2中，设DK交BH于J，连接JF．
∵DF=DB，DK⊥FB，
∴FK=BK，
∴JF=JB，
∴∠JFB=∠JBF，
∵∠JFB+∠JFH=90°，∠JBF+∠BHF=90°，
∴∠JFH=∠JHF，
∵DK⊥BF，BG⊥DF，
∴FJ⊥DB，
∵AD⊥BD，
∴AD∥FJ，
∵AF∥DJ，
∴四边形AFJD是平行四边形，
∵AH=2FH，
∴可以假设HF=a，AH=2a，
∴DJ=AF=3a，
∵FH∥DJ，

∴，设GH=m，GJ=3m，则JH=JF=JB=4m，

∴GF==m，

∵∠C=∠BFG，
∴tanC=tan∠BFG===，

∴=，

∵CD=1，
∴AD=FJ=BJ=，

∴4m=

∴m=，

∴BG=7m=.