题目内容
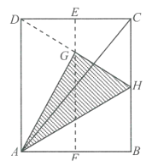
【题目】如图，在一张矩形纸片
中，对角线
，点
分别是
和
的中点，现将这张纸片折叠，使点
落在
上的点
处，折痕为
，若
的延长线恰好经过点
，则点到对角线
的距离为（ ）
.
A.
B.
C.
D.
【答案】B
【解析】
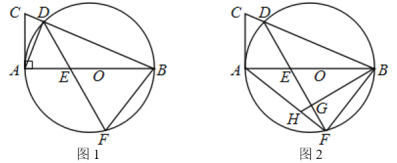
设DH与AC交于点M，易得EG为△CDH的中位线，所以DG=HG，然后证明△ADG≌△AHG，可得AD=AH，∠DAG=∠HAG，可推出∠BAH=∠HAG=∠DAG=30°，然后设BH=a，则BC=AD=AH=2a，利用勾股定理建立方程可求出a，然后在Rt△AGM中，求出GM，AG，再求斜边AM上的高即为G到AC的距离.
如图，设DH与AC交于点M，过G作GN⊥AC于N，
∵E、F分别是CD和AB的中点，
∴EF∥BC
∴EG为△CDH的中位线
∴DG=HG
由折叠的性质可知∠AGH=∠B=90°
∴∠AGD=∠AGH=90°
在△ADG和△AHG中，
∵DG=HG，∠AGD=∠AGH，AG=AG
∴△ADG≌△AHG（SAS）
∴AD=AH，AG=AB，∠DAG=∠HAG
由折叠的性质可知∠HAG=∠BAH，
∴∠BAH=∠HAG=∠DAG=
∠BAD=30°
设BH=a，
在Rt△ABH中，∠BAH=30°
∴AH=2a
∴BC=AD=AH=2a，AB=
在Rt△ABC中，AB2+BC2=AC2
即
解得
∴DH=2GH=2BH=
，AG=AB=
∵CH∥AD
∴△CHM∽△ADM
∴
∴AM=
AC=
，HM=DH=
∴GM=GH-HM=
在Rt△AGM中，
∴
故选B.
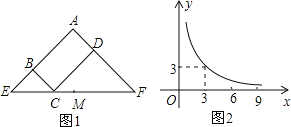
【题目】数学活动课上，老师提出问题:如图1，有一张长
,宽
的长方形纸板,在纸板的四个角裁去四个相同的小正方形，然后把四边折起来，做成-一个无盖的盒子，问小正方形的边长为多少时，盒子的体积最大.下 面是探究过程，请补充完整:
（1）设小正方形的边长为
，体积为
，根据长方体的体积公式得到
和
的关系式 ;
（2）确定自变量的取值范围是
（3）列出与的几组对应值.
| ··· |
|
|
|
|
|
|
|
|
|
|
| ··· |
|
|
|
|
|
|
|
|
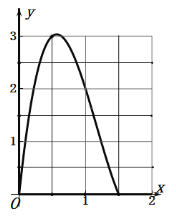
（4）在平面直角坐标系
中，描出以补全后的表中各对对应值为坐标的点画出该函数的图象如图2，结合画出的函数图象，当小正方形的边长约为 时， 盒子的体积最大，最大值约为
.(估读值时精确到
)
