Question

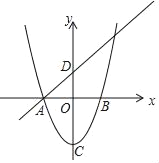
【题目】如图，已知抛物线y＝x2﹣4与x轴交于点A，B（点A位于点B的左侧），C为顶点，直线y＝x+m经过点A，与y轴交于点D．

（1）求线段AD的长；

（2）平移该抛物线得到一条新拋物线，设新抛物线的顶点为C′．若新抛物线经过点D，并且新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD，求新抛物线对应的函数表达式．

Answer 1

【答案】（1）2 ;(2) y＝x2﹣4x+2或y＝x2+6x+2．

【解析】

（1）解方程求出点A的坐标，根据勾股定理计算即可；

（2）设新抛物线对应的函数表达式为：y＝x2+bx+2，根据二次函数的性质求出点C′的坐标，根据题意求出直线CC′的解析式，代入计算即可．

解：（1）由x2﹣4＝0得，x1＝﹣2，x2＝2，

∵点A位于点B的左侧，

∴A（﹣2，0），

∵直线y＝x+m经过点A，

∴﹣2+m＝0，

解得，m＝2，

∴点D的坐标为（0，2），

∴AD＝＝2；

（2）设新抛物线对应的函数表达式为：y＝x2+bx+2，

y＝x2+bx+2＝（x+）2+2﹣，

则点C′的坐标为（﹣，2﹣），

∵CC′平行于直线AD，且经过C（0，﹣4），

∴直线CC′的解析式为：y＝x﹣4，

∴2﹣＝﹣﹣4，

解得，b1＝﹣4，b2＝6，

∴新抛物线对应的函数表达式为：y＝x2﹣4x+2或y＝x2+6x+2．