Question

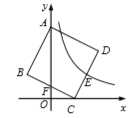
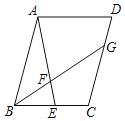
【题目】如图，在ABCD中，点E是BC边上的中点，G为线段CD上一动点，连接BG，交AE于点F，若＝m+1，则的值为__．

Answer 1

【答案】

【解析】

过E作EH∥AB，EH交BG于H，根据相似三角形的判定得出△HEF∽△BAF，△BEH∽△BCG，根据相似得出比例式，求出AB和CG，再求出DG，即可求出答案．

如图，过E作EH∥AB，EH交BG于H，

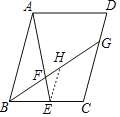
∵四边形ABCD是平行四边形，

∴AB＝CD，AB∥CD，

∴EH∥CD∥AB，

∴△HEF∽△BAF，△BEH∽△BCG，

∴， ，

∵点E是BC边上的中点， ＝m+1，

∴AB＝（m+1）EH，CG＝2EH，

∴CD＝（m+1）EH，

∴DG＝CD﹣CG＝（m+1）EH﹣2EH＝（m﹣1）EH，

∴，

故答案为：．