Question

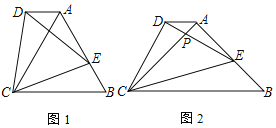
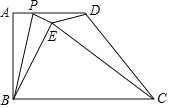
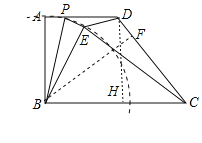
【题目】如图，四边形ABCD中，AD∥BC，AB⊥BC，点P是边AD上一动点，将△ABP沿BP折叠得到△BEP，连接DE，CE，已知AB＝4，AD＝3，BC＝6，则△CDE面积的最小值为_____．

Answer 1

【答案】2．

【解析】

如图，过点D作DH⊥BC，过点B作BF⊥CD，可证四边形ABHD是矩形，可得AB=DH=4，AD=BH=3，由勾股定理可求CD的长，由锐角三角函数可求BF的长，由点E在以B点为圆心，AB长为半径的圆上，可得当点E在BF上时，点E到CD的距离最小，即可求解．

解：如图，过点D作DH⊥BC，过点B作BF⊥CD，

∵AD∥BC，AB⊥BC，

∴AD⊥AB，且DH⊥BC，AB⊥BC，

∴四边形ABHD是矩形，

∴AB＝DH＝4，AD＝BH＝3，

∴CH＝BC﹣BH＝3，

∴CD＝，

∵sin∠DCH＝，

∴，

∴BF＝，

∵将△ABP沿BP折叠得到△BEP，

∴AB＝BE＝4，

∴点E在以B点为圆心，AB长为半径的圆上，

∴当点E在BF上时，点E到CD的距离最小，最小值＝﹣4＝，

∴△CDE面积的最小值＝；

故答案为：2．