Question

【题目】如图，二次函数y＝ax2+4x+c（a≠0）的图象与x轴交A，B两点，与y轴交于点C，直线y＝﹣2x﹣6经过点A，C．

（1）求该二次函数的解析式；

（2）点P为第三象限内抛物线上的一个动点，△APC的面积为S，试求S的最大值；

（3）若P为抛物线的顶点，且直角三角形APQ的直角顶点Q在y轴上，请直接写出点Q的坐标．

Answer 1

【答案】（1）y＝2x2+4x﹣6；（2）；（3）点Q的坐标为（0，﹣4+）或（0，﹣4﹣）．

【解析】

（1）先利用直线与坐标轴相交求得A、C坐标，再代入解析式求出a、c的值即可得；

（2）过点P作x轴的垂线与AC交于点H，设点P的横坐标为m，得HP＝﹣2m2﹣6m，再根据S＝S△APC＝S△APH+S△CPH列出关于m的函数解析式，依据二次函数的性质求解可得；

（3）作PD⊥y轴，设OQ＝m，知OD＝8，PD＝1，QD＝8﹣m，证△AOQ∽△QDP得，即，解之求出m的值可得答案．

解：（1）当 x＝0 时，y＝﹣2x﹣6＝﹣6，则 C（0，﹣6），

当 y＝0 时，﹣2x﹣6＝0，

解得 x＝﹣3，则 A（﹣3，0），

把 A（﹣3，0），C（0，﹣6）代入y＝ax2+4x+c，得，

解得：，

∴抛物线解析式为y＝2x2+4x﹣6；

（2）如图1，过点P作x轴的垂线与AC交于点H．

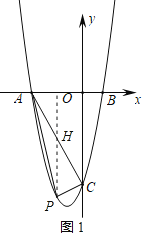
设点P的横坐标为m，

由直线AC：y＝﹣2x﹣6，可得H（m，﹣2m﹣6）．

又因为P（m，2m2+4m﹣6），所以HP＝﹣2m2﹣6m．

因为△PAH 与△PCH 有公共底边HP，高的和为A、C 两点间的水平距离3，

所以S＝S△APC＝S△APH+S△CPH＝（﹣2m2﹣6m）＝﹣3（m+）2+，

∴当m＝时，S取得最大值，最大值为；

（3）如图2，过点P作PD⊥y轴于点D，设OQ＝m，

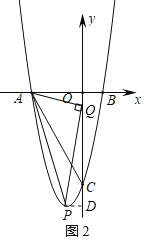
则∠AOQ＝∠PDQ＝90°，

∵y＝2x2+4x﹣6＝2（x+1）2﹣8，

∴P（﹣1，﹣8），

则OD＝8，PD＝1，QD＝8﹣m，

∵A（﹣3，0），

∴OA＝3，

∵∠AQP＝90°，

∴∠AQO+∠PQD＝90°，

∵∠AQO+∠QAO＝90°，

∴∠QAO＝∠PQD，

∴△AOQ∽△QDP，

∴，即，

解得：m＝4±，

∴点Q的坐标为（0，﹣4+）或（0，﹣4﹣）．