题目内容
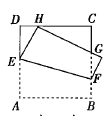
【题目】如图1,在Rt△ABC中,∠B=90°,AB=BC=12cm,点D从点A出发沿边AB以2cm/s的速度向点B移动,移动过程中始终保持DE∥BC,DF∥AC(点E、F分别在AC、BC上).设点D移动的时间为t秒.
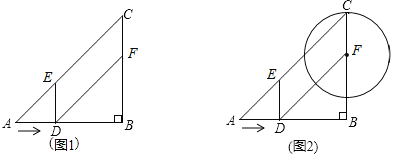
(1)试判断四边形DFCE的形状,并说明理由;
(2)当t为何值时,四边形DFCE的面积等于20cm2?
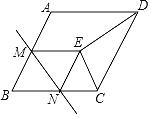
(3)如图2,以点F为圆心,FC的长为半径作⊙F,在运动过程中,当⊙F与四边形DFCE只有1个公共点时,请直接写出t的取值范围.
【答案】(1)平行四边形,理由见解析;(2)1秒或5秒;(3)12﹣6![]() <t<6
<t<6
【解析】
(1)由两组对边平行的四边形是平行四边形可证四边形DFCE是平行四边形;
(2)设点D出t秒后四边形DFCE的面积为20cm2,利用BD×CF=四边形DFCE的面积,列方程解答即可;
(3)如图2中,当点D在⊙F上时,⊙F与四边形DECF有两个公共点,求出此时t的值,根据图象即可解决问题.
解:(1)∵DE∥BC,DF∥AC,
∴四边形DFCE是平行四边形;
(2)如图1中,设点D出发t秒后四边形DFCE的面积为20cm2,根据题意得,
DE=AD=2t,BD=12﹣2t,CF=DE=2t,
又∵BD×CF=四边形DFCE的面积,
∴2t(12﹣2t)=20,
t2﹣6t+5=0,
(t﹣1)(t﹣5)=0,
解得t1=1,t2=5;
答:点D出发1秒或5秒后四边形DFCE的面积为20cm2;
(3)如图2中,当点D在⊙F上时,⊙F与四边形DECF有两个公共点,
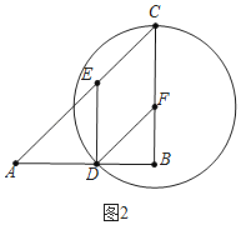
在Rt△DFB中,∵∠B=90°,AD=DF=CF=2t,BD=BF=12﹣2t,
∴2t=![]() (12﹣2t),
(12﹣2t),
∴t=12﹣6![]() ,
,
由图象可知,当12﹣6![]() <t<6时,⊙F与四边形DFCE有1个公共点.
<t<6时,⊙F与四边形DFCE有1个公共点.

【题目】甲乙两位同学参加数学综合素质测试,各项成绩如下表:(单位:分)
数与代数 | 空间与图形 | 统计与概率 | 综合与实践 | |
学生甲 | 93 | 93 | 89 | 90 |
学生乙 | 94 | 92 | 94 | 86 |
(1)分别计算甲、乙同学成绩的中位数;
(2)如果数与代数,空间与图形,统计与概率,综合与实践的成绩按4:3:1:2计算,那么甲、乙同学的数学综合素质成绩分别为多少分?