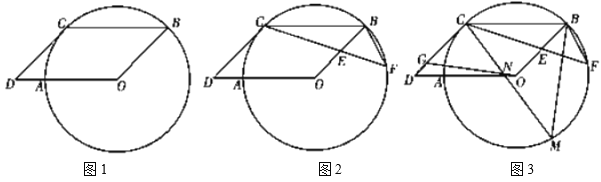
��Ŀ����
����Ŀ����֪��ACB�͡�ADE���ǵ���ֱ�������Σ���ACB����ADE��90�㣬��CE��BCΪ����ƽ���ı���CEFB����CD��CF��
��1����ͼ1����E��D�ֱ���AC��AB��ʱ����֤��CD��![]() CF��
CF��
��2����ͼ2����ADE�Ƶ�A��תһ���Ƕȣ��жϣ�1����CD��CF��������ϵ�Ƿ���Ȼ������������֤����
��3����ͼ3��AE��![]() ��AB��
��AB��![]() ������ADE��A����תһ�ܣ����ı���CEFBΪ����ʱ��ֱ��д��CF�ij���
������ADE��A����תһ�ܣ����ı���CEFBΪ����ʱ��ֱ��д��CF�ij���
���𰸡���1�������������2�����������������������3��CF��ֵΪ6��4��
��������
��1������FD��֤����ADC�ա�EDF��SAS�����Ƴ���DFCΪ����ֱ�������μ��ɽ�����⣻
��2������������FD��֤����ADC�ա�EDF��SAS�����Ƴ���DFCΪ����ֱ�������μ��ɽ�����⣻
��3�����������ηֱ�ͼ�Σ����ã�2���н������CD���ɽ�����⣮
��1��֤��������FD��
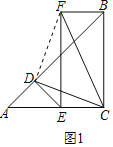
��AD��ED����ADE��90����
���DAC����AED��45����
���ı���BCEF��ƽ���ı��Σ���BCE��90����
���ı���BCEF�Ǿ��Σ�
���CEF����AEF��90����BC��EF��AC��
���DEF��45����
���A����DEF��
���ADC�ա�EDF��SAS����
��DC��DF����DCA����DFE��
���FDC����FEC��90�����Ӷ���DFCΪ����ֱ�������Σ�
��CD��![]() CF��
CF��
��2���⣺������
���ɣ�����FD��
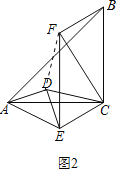
��AD��DE��EF��AC��
���DAC����DEF����AD��ED��AC��EF��
���ADC�ա�EDF��SAS����
��DC��DF����ADC����EDF������ADE+��EDC����FDC+��EDC��
���FDC����ADE��90����
���DFCΪ����ֱ�������Σ�
��CD��![]() CF��
CF��
��3���⣺��ͼ3��1�У���AE��CD�Ľ���ΪM��
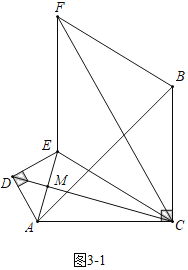
��CE��CA��DE��DA��
��CD��ֱƽ��AE��
��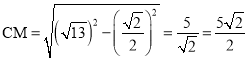 ��DM��
��DM��![]() ��
��
��CD��DM+CM��![]() ��
��
��CF��![]() CD
CD
��CF��6��
��ͼ3��2�У���AE��CD�Ľ���ΪM��
ͬ���ɵ�CD��CM��DM��![]() ��
��
��CF��![]() CD��4��
CD��4��
��������������������CF��ֵΪ6��4��

 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д�