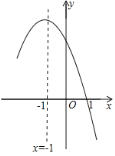Question

【题目】如图，已知是的直径，切于点，交于另一点．

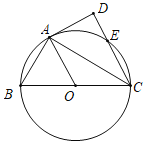
（1）求证：；

（2）若是上一动点，则

①当 时，以，，，为顶点的四边形是正方形；

②当 时，以，，，为顶点的四边形是菱形．

Answer 1

【答案】（1）证明见解析；（2）①；②30°或．

【解析】

（1）根据是的直径，切于点，，可得=90°，=∠ACO，即可证明△ACD∽△BCA；

（2）①若四边形A、O、C、D为正方形，可得∠AOC=90°，由OA=OC，得到∠OCA=∠OAC=45°，进而可得∠B=45°；

②若四边形A、O、C、E为菱形，分二种情况讨论：分点E与点A同侧；点E与点A异侧分别求解即可．

（1）证明：∵切于点，

∴，

∵，

∴，，

∵是的直径，，

∴，，

∴，

∴，

∴；

（2）①若四边形AOCD为正方形，

∴∠AOC=90°，

∵OA=OC，

∴∠OCA=∠OAC=45°，

∵∠BAC=90°，

∴∠B=90°-45°=45°，

故答案为：45°；

②若四边形A、O、C、E为菱形，分二种情况讨论：分点E与点A同侧；点E与点A异侧，

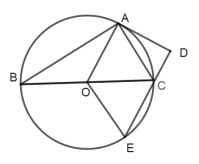
当点E与点A同侧时，连接AE，如图所示：

∵AD为切线，

∴∠DAE=∠ECA，∠OAD=90°，

∵AOCE为菱形，

∴∠OAC=∠EAC，

∴∠DAE=∠ECA=∠OAC=30°，

∴∠ACO=30°，∠AOB=∠ACO+∠OAC=30°+30°=60°，

∵OA=OB，

∴∠B=60°；

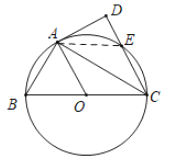
当点E与点A异侧时，如图所示：

∵AOEC是菱形，

∴AC=AO=OC，

∴△AOC是等边三角形，

∴∠AOC=60°，

∵AO=BO，

∴∠B=∠BAO=30°，

综上所述，∠B为30°或60°，

故答案为：30°或60°．