题目内容
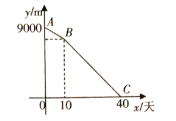
【题目】某街道需要铺设管线的总长为9000
，计划由甲队施工，每天完成150．工作一段时间后，因为天气原因，想要40天完工，所以增加了乙队．如图表示剩余管线的长度
与甲队工作时间
（天）之间的函数关系图象．
（1）直接写出点
的坐标；
（2）求线段
所对应的函数解析式，并写出自变量的取值范围；
（3）直接写出乙队工作25天后剩余管线的长度．
【答案】（1）（10，7500）（2）直线BC的解析式为y=-250x+10000，自变量x的取值范围为10≤x≤40.（3）1250米.
【解析】
（1）由于前面10天由甲单独完成，用总的长度减去已完成的长度即为剩余的长度，从而求出点B的坐标；（2）利用待定系数法求解即可；（3）已队工作25天后，即甲队工作了35天，故当x=35时，函数值即为所求.
（1）9000-150×10=7500.
∴点B的坐标为（10，7500）
（2）设直线BC的解析式为y=kx+b，依题意，得：
解得：
∴直线BC的解析式为y=-250x+10000，
∵乙队是10天之后加入，40天完成，
∴自变量x的取值范围为10≤x≤40.
（3）依题意，当x=35时，y=-250×35+10000=1250.
∴乙队工作25天后剩余管线的长度是1250米.
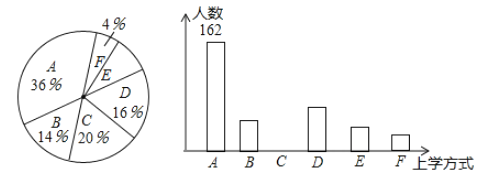
【题目】体育理化考试前夕，九（2）班组织了体育理化考试模拟（体育+理化=100分），模拟测试后相关负责人对成绩进行了统计，制作如下频数分布表和频数分布直方图，请根据表中信息解答问题：
分数段（ | 频数 | 频率 |
| 5 | 0．1 |
| 5 |
|
|
| 0．4 |
| 15 | 0．3 |
| 5 | 0．1 |
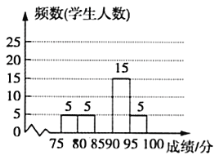
（1）表中
________，
________，并补全直方图；
（2）若用扇形统计图描述此成绩分布情况，则分数段
所对应扇形的圆心角度数是_____；
（3）若该校九年级共950名学生，请估计该年级分数在
的学生有多少人？
