Question

【题目】抛物线y=x2-(m+1)x+m与y轴交于(0，-3)点.

(1)求出m的值和抛物线与x轴的交点；

(2)x取什么值时，y>0.

Answer 1

【答案】(1) m=-3，(-3，0)和(1，0)；(2)x<-3或x>1.

【解析】

(1)将点(0，-3)代入函数解析式，可求出m的值，得到抛物线解析式，令y=0得到关于x的一元二次方程，解方程即可得到抛物线与x轴的交点坐标.

(2)利用二次函数的性质，可知抛物线的开口向上，再根据抛物线与x轴的两交点的横坐标，可得到y＞0时，x的取值范围.

解：(1)把(0,-3)代入y=x2-(m+1)x+m，得m=-3

∴抛物线解析式为y=x2+2x-3

令y=0，得x2+2x-3=0，解得x1=-3，x2=1

∴抛物线与x轴的交点为(-3,0)和(1,0)

(2)如图所示，

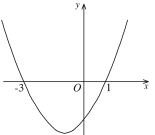
∵抛物线开口向上，

∴当x<-3或x>1时，y>0