题目内容
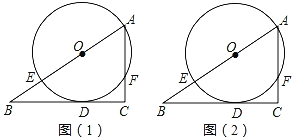
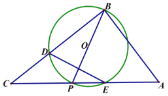
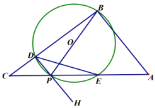
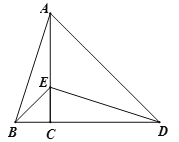
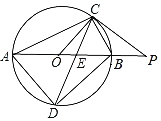
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,连接AC、BC,过点C作∠BCP=∠BAC,交AB的延长线于点P,弦CD平分∠ACB,交AB于点E,连接OC、AD、BD.
(1)求证:PC为⊙O的切线;
(2)若OC=5,OE=1,求PC的长.
【答案】(1)证明见解性;(2)PC=12
【解析】
(1)根据圆周角定理和等腰三角形的性质证得OC⊥PC,即可证得结论;
(2)证明∠PEC=∠PCE,根据等角对等边可得PE=PC,设PC=PE=x,则OP=x+1,根据勾股定理即可求得.
(1)证明:∵OB=OC,
∴∠OBC=∠OCB,
∵AB是⊙O的直径,
∴∠ACB=90°
∴∠BAC+∠OBC=90°,
∵∠BCP=∠BAC,
∴∠OCB+∠BCP=90°,即∠OCP=90°,
∴OC⊥PC,
∴PC为⊙O的切线;
(2)解:∵CD平分∠ACB,
∴∠ACD=∠BCD
∴![]() =
=![]() ,
,
∴∠ABD=∠DCB,
∵∠BCP=∠BAC,∠BAC=∠BDC,∠BAD=∠BCD,
∴∠PCB=∠BDC,∠ABD=∠BCD,
∴∠BDC+∠ABD=∠BCD+∠PCB,即∠PEC=∠PCE,
∴PC=PE,
设PC=PE=x,则OP=x+1,
在Rt△OPC中,OP2=OC2+PC2,
∴(x+1)2=52+x2,
解得x=12,
∴PC=12.

 世纪百通期末金卷系列答案
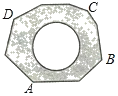
世纪百通期末金卷系列答案【题目】如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为2米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:
掷小石子落在不规则图形内的总次数 | 50 | 150 | 300 | … |
小石子落在圆内(含圆上)的次数m | 20 | 59 | 123 | … |
小石子落在圆外的阴影部分(含外缘)的次数n | 29 | 91 | 176 | … |
(1)当投掷的次数很大时,则m:n的值越来越接近 (结果精确到0.1)
(2)若以小石子所落的有效区域为总数(即m+n),则随着投掷次数的增大,小石子落在圆内(含圆上)的频率值稳定在 附近(结果精确到0.1);
(3)请你利用(2)中所得频率的值,估计整个封闭图形ABCD的面积是多少平方米?(结果保留π)
【题目】下表显示的是某种大豆在相同条件下的发芽试验结果:
每批粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
发芽的粒数m | 96 | 282 | 382 | 570 | 948 | 1904 | 2850 |
发芽的频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.952 | 0.950 |
下面有三个推断:
①当n为400时,发芽的大豆粒数为382,发芽的频率为0.955,所以大豆发芽的概率是0.955;
②随着试验时大豆的粒数的增加,大豆发芽的频率总在0.95附近摆动,显示出一定的稳定性,可以估计大豆发芽的概率是0.95;
③若大豆粒数n为4000,估计大豆发芽的粒数大约为3800粒.
其中推断合理的是( )
A. ①②③ B. ①② C. ①③ D. ②③