题目内容
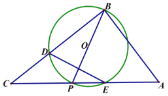
【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB,连接DO并延长交CB的延长线于点E,连接OC.
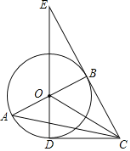
(1) 判断直线CD与⊙O的位置关系,并说明理由;
(2) 若BE=![]() ,DE=3,求⊙O的半径及AC的长.
,DE=3,求⊙O的半径及AC的长.
【答案】(1)DC是⊙O的切线,理由见解析;(2)半径为1,AC=![]()
【解析】
(1)欲证明CD是切线,只要证明OD⊥CD,利用全等三角形的性质即可证明;
(2)设⊙O的半径为r.在Rt△OBE中,根据OE2=EB2+OB2,可得![]() ,推出r=1,可得OE=2,即有
,推出r=1,可得OE=2,即有![]() ,可推出
,可推出![]() ,则利用勾股定理和含有30°的直角三角形的性质,可求得OC=2,
,则利用勾股定理和含有30°的直角三角形的性质,可求得OC=2,![]() ,再利用勾股定理求出
,再利用勾股定理求出![]() 即可解决问题;
即可解决问题;
(1)证明:∵CB=CD,CO=CO,OB=OD,
∴△OCB≌△OCD(SSS),
∴∠ODC=∠OBC=90°,
∴OD⊥DC,
∴DC是⊙O的切线;
(2)解: 设⊙O的半径为r.
在Rt△OBE中,∵OE2=EB2+OB2,
∴![]() ,
,
∴![]()
∴OE=3-1=2
Rt△ABC中,![]()
∴![]()
∴![]()
![]()
Rt△BCO中,![]() ,
,
![]()
Rt△ABC中,![]()

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目