题目内容
【题目】关于的一元二次方程x2+2x+k+1=0的实数解是x1和x2.
(1)求k的取值范围;
(2)如果x1+x2﹣x1x2<﹣1且k为整数,求k的值.
【答案】解:(1)k≤0.(2)k的值为﹣1和0.
【解析】
(1)方程有两个实数根,必须满足△=b2-4ac≥0,从而求出实数k的取值范围;(2)先由一元二次方程根与系数的关系,得x1+x2=-2,x1x2=k+1.再代入不等式x1+x2-x1x2<-1,即可求得k的取值范围,然后根据k为整数,求出k的值.
(1)∵方程有实数根,
∴△=224(k+1)≥0,
解得k ≤0.
故k的取值范围是k≤0.
(2)根据一元二次方程根与系数的关系,得![]() =2,
=2,![]() =k+1,
=k+1,
![]()
![]() =2(k+1).
=2(k+1).
由已知,得2(k+1)<1,解得k>2.
又由(1)k≤0,
∴2<k≤0.
∵k为整数,
∴k的值为1或0.

练习册系列答案
相关题目
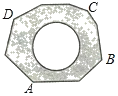
【题目】如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为2米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:
掷小石子落在不规则图形内的总次数 | 50 | 150 | 300 | … |
小石子落在圆内(含圆上)的次数m | 20 | 59 | 123 | … |
小石子落在圆外的阴影部分(含外缘)的次数n | 29 | 91 | 176 | … |
(1)当投掷的次数很大时,则m:n的值越来越接近 (结果精确到0.1)
(2)若以小石子所落的有效区域为总数(即m+n),则随着投掷次数的增大,小石子落在圆内(含圆上)的频率值稳定在 附近(结果精确到0.1);
(3)请你利用(2)中所得频率的值,估计整个封闭图形ABCD的面积是多少平方米?(结果保留π)