��Ŀ����
����Ŀ����ͼ��������y����x+2��2+m��x�ύ��A��B���㣬��y�ύ�ڵ�C����D���������ϣ������C���������ߵĶԳ���Գƣ������ߵĶ���ΪM����B������Ϊ����1��0����
��1���������ߵĽ���ʽ��A��C��D�����ꣻ
��2���ж���ABM����״����֤����Ľ��ۣ�
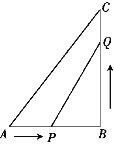
��3������P��ֱ��BD��һ�����㣬�Ƿ������P��C��DΪ���������������ABD���ƣ������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵������
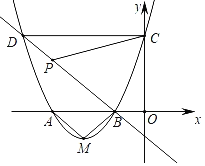
���𰸡���1���������ߵĽ���ʽΪy����x+2��2��1��A����3��0����C��0��3����D����4��3������2����ABM�ǵ���ֱ�������Σ�����������3�����ڣ����ɼ�������
��������
��1����B����1��0�����������߽���ʽ����������ߵĽ���ʽ���ֱ���x=0��y=0�����A��C�����꣬��������������ԳƵ����ʿ����D�����ꣻ
��2����MN��x�ᣬ��������������ԳƵ������Լ�����ǵ����Ǻ�������á�MAN����MBN��45�����Ӷ��õ���ABM�ǵ���ֱ�������Σ�
��3����Ҫ�������ۣ���ABD�ס�PDC����ABD�ס�CDP���������������ε��������![]() �ij��ȣ�Ȼ�����õ�
�ij��ȣ�Ȼ�����õ�![]() �����꣮
�����꣮
�⣺��1����B����1��0�����������߽���ʽ�ã�
����1+2��2+m��0��
���m����1��
�������ߵĽ���ʽΪy����x+2��2��1��
��y��0ʱ����x+2��2��1��0�����x1����1��x2����3��
��A����3��0����
��x��0ʱ��y����x+2��2��1��3��
��C��0��3��
�������߶Գ�����ֱ��x����2��C��D������������߶Գ���Գƣ�
��D����4��3����
��2����ABM�ǵ���ֱ�������Σ�
֤������������y����x+2��2��1�Ķ�����M��
��M����2����1����
��MN��x����N����N����2��0����
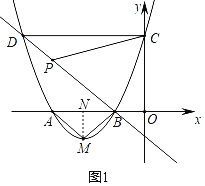
��AN��BN��MN��1��
��AM��BM��
tan��MAN��tan��MBN��1��
���MAN����MBN��45����
���AMB��180������MAN����MBN��90����
���ABM�ǵ���ֱ�������Σ�
��3�����ڣ����ɣ�
�ٵ���ABD�ס�PDCʱ��
![]() ������
������![]() ��
��
��PD��![]() ��
��
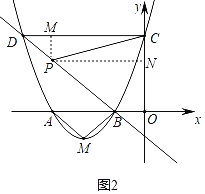
����P�ֱ���x��y��Ĵ��߽��ڵ�M��N��
��PM��![]() ��DM��
��DM��
���P��![]() ��
��![]() ����
����
�ڵ���ABD�ס�CDPʱ��
ͬ���ɵã���P��2����3��
���ϣ���P��![]() ��
��![]() ����P2��2����3��
����P2��2����3��

 ��ѧ����ϵ�д�
��ѧ����ϵ�д�