题目内容
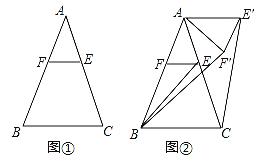
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,将
的中点,将![]() 绕点
绕点![]() 旋转,当
旋转,当![]() (即
(即![]() )与
)与![]() 交于一点
交于一点![]() ,
,![]() (
(![]() )同时与
)同时与![]() 交于一点
交于一点![]() 时,点
时,点![]() ,
,![]() 和点
和点![]() 构成
构成![]() ,在此过程中,
,在此过程中,![]() 周长的最小值是__________.
周长的最小值是__________.
【答案】![]()
【解析】
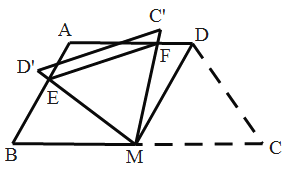
连接AM,过点D作DN⊥CM于N,AQ⊥BM于Q,首先易证四边形AQND是平行四边形,四边形ABCD是等腰梯形,然后根据含30度直角三角形的性质可得CN=2,BQ=2,求出CM=CD,证明△CMD、△ABM、△AMD是等边三角形,然后可得∠BME=∠AMF,利用ASA证明△BME≌△AMF,求出BE=AF,即可得到AE+AF=AE+BE=AB=4,故当ME最短时,![]() 的周长最小,此时ME⊥AB,根据等边三角形的性质和勾股定理求出ME即可.
的周长最小,此时ME⊥AB,根据等边三角形的性质和勾股定理求出ME即可.
解:如图,连接AM,过点D作DN⊥CM于N,AQ⊥BM于Q,
∴AQ∥DN,
∵AD∥BC,![]() ,
,
∴四边形AQND是平行四边形,四边形ABCD是等腰梯形,
∴QN=AD=4,![]() ,
,
∴CN=![]() ,BQ=
,BQ=![]() ,
,
∴BC=BQ+QN+CN=2+4+2=8,即BC=2CD,
∵![]() 是
是![]() 的中点,
的中点,
∴CM=CD,
∴△CMD是等边三角形,
同理可得△ABM是等边三角形,
∴△AMD是等边三角形,
∴∠BMA=∠DMC=∠EMF=60°,
∴∠BME=∠AMF,
在△BME和△AMF中,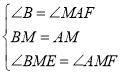 ,
,
∴△BME≌△AMF(ASA),
∴BE=AF,
∴AE+AF=AE+BE=AB=4,
∴当ME最短时,![]() 的周长最小,
的周长最小,
即ME⊥AB时,![]() 的周长最小,
的周长最小,
∵△ABM是等边三角形,BM=AM=4,
∴ME⊥AB时,BE=2,
∴![]() ,
,
∴△AEF的周长最小值为![]() ,
,
故答案为:![]() .
.

 优加精卷系列答案
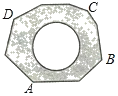
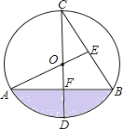
优加精卷系列答案【题目】如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为2米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:
掷小石子落在不规则图形内的总次数 | 50 | 150 | 300 | … |
小石子落在圆内(含圆上)的次数m | 20 | 59 | 123 | … |
小石子落在圆外的阴影部分(含外缘)的次数n | 29 | 91 | 176 | … |
(1)当投掷的次数很大时,则m:n的值越来越接近 (结果精确到0.1)
(2)若以小石子所落的有效区域为总数(即m+n),则随着投掷次数的增大,小石子落在圆内(含圆上)的频率值稳定在 附近(结果精确到0.1);
(3)请你利用(2)中所得频率的值,估计整个封闭图形ABCD的面积是多少平方米?(结果保留π)