题目内容
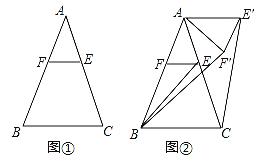
【题目】“如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.”这里,根据已学的相似三角形的知识,易证:![]() =
=![]() .在图1这个基本图形的基础上,继续添加条件“如图2,点E是直线AC上一动点,连接DE,过点D作FD⊥ED,交直线BC于点F,设
.在图1这个基本图形的基础上,继续添加条件“如图2,点E是直线AC上一动点,连接DE,过点D作FD⊥ED,交直线BC于点F,设![]() =
=![]() .”
.”
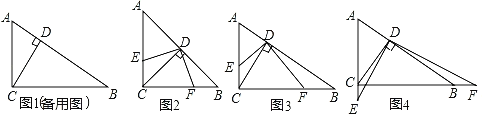
(1)探究发现:如图②,若m=n,点E在线段AC上,则![]() = ;
= ;
(2)数学思考:
①如图3,若点E在线段AC上,则![]() = (用含m,n的代数式表示);
= (用含m,n的代数式表示);
②当点E在直线AC上运动时,①中的结论是否仍然成立?请仅就图4的情形给出证明;
(3)拓展应用:若AC=![]() ,BC=2
,BC=2![]() ,DF=4
,DF=4![]() ,请直接写出CE的长.
,请直接写出CE的长.
【答案】(1)1;(2)①![]() ;②成立,理由见解析;(3)CE=2
;②成立,理由见解析;(3)CE=2![]() 或CE=
或CE=![]()
【解析】
(1)先用等量代换判断出∠ADE=∠CDF,∠A=∠DCB,得到△ADE∽△CDF,再判断出△ADC∽△CDB即可.
(2)方法和(1)一样,先用等量代换判断出∠ADE=∠CDF,∠A=∠DCB,得到△ADE∽△CDF,再判断出△ADC∽△CDB即可.
(3)由(2)的结论得出△ADE∽△CDF,判断出CF=2AE,求出EF,再利用勾股定理,分三种情形分别求解即可.
(1)当m=n时,即:BC=AC,
∵∠ACB=90°,
∴∠A+∠ABC=90°,
∵CD⊥AB,
∴∠DCB+∠ABC=90°,
∴∠A=∠DCB,
∵∠FDE=∠ADC=90°,
∴∠FDE﹣∠CDE=∠ADC﹣∠CDE,
即∠ADE=∠CDF,
∴△ADE∽△CDF,
∴![]() =
=![]() ,
,
∵∠A=∠DCB,∠ADC=∠BDC=90°,
∴△ADC∽△CDB,
∴![]() =
=![]() =1,
=1,
∴![]() =1,
=1,
故答案为1.
(2)①∵∠ACB=90°,
∴∠A+∠ABC=90°,
∵CD⊥AB,
∴∠DCB+∠ABC=90°,
∴∠A=∠DCB,
∵∠FDE=∠ADC=90°,
∴∠FDE﹣∠CDE=∠ADC﹣∠CDE,
即∠ADE=∠CDF,
∴△ADE∽△CDF,
∴![]() =
=![]() ,
,
∵∠A=∠DCB,∠ADC=∠BDC=90°,
∴△ADC∽△CDB,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
故答案为![]() .
.
②成立.如图,
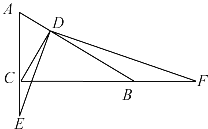
∵∠ACB=90°,
∴∠A+∠ABC=90°,
又∵CD⊥AB,
∴∠DCB+∠ABC=90°,
∴∠A=∠DCB,
∵∠FDE=∠ADC=90°,
∴∠FDE+∠CDE=∠ADC+∠CDE,
即∠ADE=∠CDF,
∴△ADE∽△CDF,
∴![]() =
=![]() ,
,
∵∠A=∠DCB,∠ADC=∠BDC=90°,
∴△ADC∽△CDB,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() .
.
(3)由(2)有,△ADE∽△CDF,
∵![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴CF=2AE,
在Rt△DEF中,DE=2![]() ,DF=4
,DF=4![]() ,
,
∴EF=![]() =
=![]() =2
=2![]() ,
,
①当E在线段AC上时,在Rt△CEF中,CF=2AE=2(AC﹣CE)=2(![]() ﹣CE),EF=2
﹣CE),EF=2![]() ,
,
根据勾股定理得,CE2+CF2=EF2,
∴CE2+[2(![]() ﹣CE)]2=40
﹣CE)]2=40
∴CE=2![]() ,或CE=﹣
,或CE=﹣![]() (舍去)
(舍去)
而AC=![]() <CE,
<CE,
∴此种情况不存在,
②当E在AC延长线上时,
在Rt△CEF中,CF=2AE=2(AC+CE)=2(![]() +CE),EF=2
+CE),EF=2![]() ,
,
根据勾股定理得,CE2+CF2=EF2,
∴CE2+[2(![]() +CE)]2=40,
+CE)]2=40,
∴CE=![]() ,或CE=﹣2
,或CE=﹣2![]() (舍),
(舍),
③如图4﹣1,当点E在CA延长线上时,
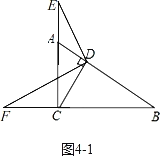
CF=2AE=2(CE﹣AC)=2(CE﹣![]() ),EF=2
),EF=2![]() ,
,
根据勾股定理得,CE2+CF2=EF2,
∴CE2+[2(CE﹣![]() )]2=40,
)]2=40,
∴CE=2![]() ,或CE=﹣
,或CE=﹣![]() (舍)
(舍)
即:CE=2![]() 或CE=
或CE=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
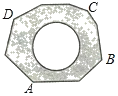
小学生10分钟应用题系列答案【题目】如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为2米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:
掷小石子落在不规则图形内的总次数 | 50 | 150 | 300 | … |
小石子落在圆内(含圆上)的次数m | 20 | 59 | 123 | … |
小石子落在圆外的阴影部分(含外缘)的次数n | 29 | 91 | 176 | … |
(1)当投掷的次数很大时,则m:n的值越来越接近 (结果精确到0.1)
(2)若以小石子所落的有效区域为总数(即m+n),则随着投掷次数的增大,小石子落在圆内(含圆上)的频率值稳定在 附近(结果精确到0.1);
(3)请你利用(2)中所得频率的值,估计整个封闭图形ABCD的面积是多少平方米?(结果保留π)
【题目】下表显示的是某种大豆在相同条件下的发芽试验结果:
每批粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
发芽的粒数m | 96 | 282 | 382 | 570 | 948 | 1904 | 2850 |
发芽的频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.952 | 0.950 |
下面有三个推断:
①当n为400时,发芽的大豆粒数为382,发芽的频率为0.955,所以大豆发芽的概率是0.955;
②随着试验时大豆的粒数的增加,大豆发芽的频率总在0.95附近摆动,显示出一定的稳定性,可以估计大豆发芽的概率是0.95;
③若大豆粒数n为4000,估计大豆发芽的粒数大约为3800粒.
其中推断合理的是( )
A. ①②③ B. ①② C. ①③ D. ②③