ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() ЃК
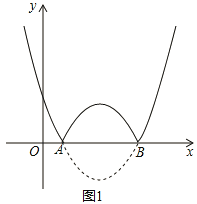
ЃК![]() гыxжсНЛгкAЃЌBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌНЋХзЮяЯпlдкxжсЯТЗНВПЗжбиxжсЗелЃЌxжсЩЯЗНЕФЭМЯёБЃГжВЛБфЃЌОЭзщГЩСЫКЏЪ§
гыxжсНЛгкAЃЌBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌНЋХзЮяЯпlдкxжсЯТЗНВПЗжбиxжсЗелЃЌxжсЩЯЗНЕФЭМЯёБЃГжВЛБфЃЌОЭзщГЩСЫКЏЪ§![]() ЕФЭМЯёЃЎ
ЕФЭМЯёЃЎ
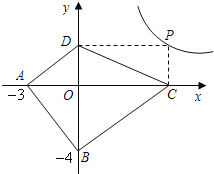
ЃЈ1ЃЉШєЕуAЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЎ
ЂйЧѓХзЮяЯп![]() ЕФБэДяЪНЃЌВЂжБНгаДГіЕБxЮЊКЮжЕЪБЃЌКЏЪ§
ЕФБэДяЪНЃЌВЂжБНгаДГіЕБxЮЊКЮжЕЪБЃЌКЏЪ§![]() ЕФжЕyЫцxЕФдіДѓЖјдіДѓЃЛ
ЕФжЕyЫцxЕФдіДѓЖјдіДѓЃЛ
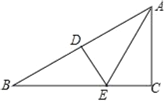
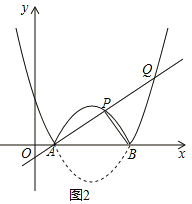
ЂкШчЭМ2ЃЌШєЙ§AЕуЕФжБЯпНЛКЏЪ§![]() ЕФЭМЯёгкСэЭтСНЕуPЃЌQЃЌЧв
ЕФЭМЯёгкСэЭтСНЕуPЃЌQЃЌЧв![]() ЃЌЧѓЕуPЕФзјБъЃЛ
ЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌШєКЏЪ§
ЪБЃЌШєКЏЪ§![]() ЕФжЕyЫцxЕФдіДѓЖјдіДѓЃЌжБНгаДГіhЕФШЁжЕЗЖЮЇЃЎ
ЕФжЕyЫцxЕФдіДѓЖјдіДѓЃЌжБНгаДГіhЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂйЕБ![]() Лђ
Лђ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() ЕФжЕyЫцxЕФдіДѓЖјдіДѓЃЌЂк PЕузјБъЮЊ
ЕФжЕyЫцxЕФдіДѓЖјдіДѓЃЌЂк PЕузјБъЮЊ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ2ЃЉЕБ
ЃЛЃЈ2ЃЉЕБ![]() Лђ
Лђ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() ЕФжЕyЫцxЕФдіДѓЖјдіДѓЃЎ
ЕФжЕyЫцxЕФдіДѓЖјдіДѓЃЎ
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉЂйРћгУД§ЖЈЯЕЪ§ЗЈЧѓХзЮяЯпЕФНтЮіЪНЃЌгЩЖдГЦадЧѓЕуBЕФзјБъЃЌИљОнЭМЯѓаДГіКЏЪ§ЕФжЕyЫцxЕФдіДѓЖјдіДѓЃЈМДГЪЩЯЩ§ЧїЪЦЃЉЕФxЕФШЁжЕЃЛ
ЂкШчЭМ2ЃЌзїИЈжњЯпЃЌЙЙНЈЖдГЦЕуFКЭжБНЧНЧШ§НЧаЮAQEЃЌИљОнSЁїABQ=2SЁїABPЃЌЕУQE=2PDЃЌжЄУїЁїPADЁзЁїQAEЃЌдђ![]() ЃЌЕУAE=2ADЃЌЩшAD=aЃЌИљОнQE=2FDСаЗНГЬПЩЧѓЕУaЕФжЕЃЌВЂМЦЫуPЕФзјБъЃЛ
ЃЌЕУAE=2ADЃЌЩшAD=aЃЌИљОнQE=2FDСаЗНГЬПЩЧѓЕУaЕФжЕЃЌВЂМЦЫуPЕФзјБъЃЛ
ЃЈ2ЃЉЯШСюy=0ЧѓХзЮяЯпгыxжсЕФСНИіНЛЕузјБъЃЌИљОнЭМЯѓжаГЪЩЯЩ§ЧїЪЦЕФВПЗжЃЌгаСНВПЗжЃКЗжБ№ЬжТлЃЌВЂСаВЛЕШЪНЛђВЛЕШЪНзщПЩЕУhЕФШЁжЕЃЎ
ЯъНтЃКЃЈ1ЃЉЂйЁпЕуAЃЈ1ЃЌ0ЃЉдкХзЮяЯп![]() ЩЯЃЌ
ЩЯЃЌ
Ёр ![]() ЃЎ
ЃЎ
НтЕУh=3Лђ![]() ЃЎ
ЃЎ
ЁпЕуAдкЕуBзѓВрЃЌ
Ёр![]() ЃЈЩсШЅЃЉЃЎ
ЃЈЩсШЅЃЉЃЎ
Ёр![]() ЃЎ
ЃЎ
Ёр ХзЮяЯпЕФБэДяЪНЮЊ![]() ЃЎ
ЃЎ
ЁрХзЮяЯпЕФЖдГЦжсЮЊжБЯп![]() ЃЎ
ЃЎ
ЁргЩЖдГЦадЕУBЃЈ5ЃЌ0ЃЉЃЎ
гЩЭМЯѓПЩжЊЃКЕБ![]() Лђ
Лђ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() ЕФжЕyЫцxЕФдіДѓЖјдіДѓЃЎ
ЕФжЕyЫцxЕФдіДѓЖјдіДѓЃЎ
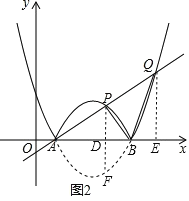
ЂкШчЭМ2ЃЌзїPDЁЭxжсгкЕуDЃЌбгГЄPDНЛХзЮяЯпlгкЕуFЃЌзїQEЁЭxжсгкЕуEЃЎ
гЩЖдГЦадПЩЕУ DF=PDЃЎ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
ЁрQE=2PDЃЎ
ЁпЁЯADP=ЁЯAEQ=90ЁуЃЌЁЯPAD=ЁЯEAQЃЎ
ЁрЁїPADЁзЁїQAEЃЎ
Ёр![]() ЃЎ
ЃЎ
ЁрAE=2ADЃЎ
ЩшAD=aЃЌдђOD=1+aЃЌOE=1+2aЃЌPЃЈ1+![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁпЕуFЃЌQдкХзЮяЯп![]() ЩЯЃЌ
ЩЯЃЌ
Ёр![]() ЃЎ
ЃЎ
![]() ЃЎ
ЃЎ
Ёр![]() ЃЎ
ЃЎ
НтЕУЃК![]() Лђ
Лђ![]() ЃЈЩсШЅЃЉЃЎ
ЃЈЩсШЅЃЉЃЎ
ЁрPЕузјБъЮЊ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЃЈ2ЃЉЕБy=0ЪБЃЌ![]() ЃЈx-hЃЉ2-2=0ЃЌ
ЃЈx-hЃЉ2-2=0ЃЌ
НтЕУЃКx=h+2Лђx=h-2ЃЌ
ЁпЕуAдкЕуBЕФзѓВрЃЌЧвh>0ЃЌ
ЁрAЃЈh-2ЃЌ0ЃЉЃЌBЃЈh+2ЃЌ0ЃЉЃЌ
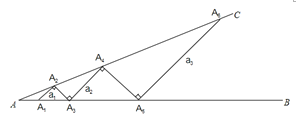
ШчЭМ3ЃЌзїХзЮяЯпЕФЖдГЦжсНЛХзЮяЯпгкЕуCЃЌ
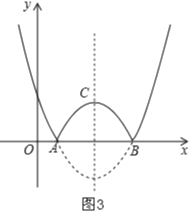
ЗжСНжжЧщПіЃК
ЂйгЩЭМЯѓПЩжЊЃКЭМЯѓfдкACЖЮЪБЃЌКЏЪ§fЕФжЕЫцxЕФдіДѓЖјдіДѓЃЌ
дђ![]() ЃЌ
ЃЌ
Ёр3ЁмhЁм4ЃЌ
ЂкгЩЭМЯѓПЩжЊЃКЭМЯѓfЕуBЕФгвВрЪБЃЌКЏЪ§fЕФжЕЫцxЕФдіДѓЖјдіДѓЃЌ
МДЃКh+2Ём2ЃЌ
hЁм0ЃЌ
злЩЯЫљЪіЃЌЕБ3ЁмhЁм4ЛђhЁм0ЪБЃЌКЏЪ§fЕФжЕЫцxЕФдіДѓЖјдіДѓЃЎ