题目内容
【题目】已知，正方形ABCD中，
，
绕点A顺时针旋转，它的两边长分别交CB、DC或它们的延长线
于点MN，
于点H．
如图
，当点A旋转到
时，请你直接写出AH与AB的数量关系；
如图
，当绕点A旋转到
时，中发现的AH与AB的数量关系还成立吗？如果不成立请写出理由，如果成立请证明．
【答案】
；（2）数量关系还成立．证明见解析.
【解析】
(1)由题意可证△ABM≌△ADN，可得AM=AN，∠BAM=∠DAN=22.5°，再证△ABM≌△AMH可得结论；
(2)延长CB至E，使BE=DN，可证△ABE≌△ADN，可得AN=AE，∠BAE=∠DAN，可得∠EAM=∠MAN=45°且AM=AM，AE=AN，可证△AME≌△AMN，则结论可证．
，理由如下：
是正方形
，
且
，
≌
，
，
，
，
，
，
，
，
，
且
，
，
≌
，
；
数量关系还成立．
如图，延长CB至E，使
，
，，
，
≌，
，
，
，
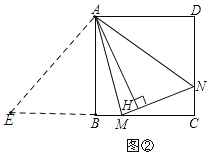
即
，
且，
，
≌
，
，
≌
，
，
.
练习册系列答案
相关题目
