ЬтФПФкШн
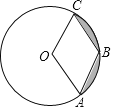
ЁОЬтФПЁПЁАОЛбяЁБЫЎОЛЛЏгаЯоЙЋЫОгУ160ЭђдЊЃЌзїЮЊаТВњЦЗЕФбаЗЂЗбгУЃЌГЩЙІбажЦГіСЫвЛжжЪаГЁМБашЕФаЁаЭЫЎОЛЛЏВњЦЗЃЌвбгкЕБФъЭЖШыЩњВњВЂНјааЯњЪлЃЎвбжЊЩњВњетжжаЁаЭЫЎОЛЛЏВњЦЗЕФГЩБОЮЊ4дЊ/МўЃЌдкЯњЪлЙ§ГЬжаЗЂЯжЃКУПФъЕФФъЯњЪлСП![]() (ЭђМў)гыЯњЪлМлИёxЃЈдЊ/МўЃЉЕФЙиЯЕШчЭМЫљЪОЃЌЦфжаABЮЊЗДБШР§КЏЪ§ЭМЯѓЕФвЛВПЗжЃЌBCЮЊвЛДЮКЏЪ§ЭМЯѓЕФвЛВПЗжЃЎЩшЙЋЫОЯњЪлетжжЫЎОЛЛЏВњЦЗЕФФъРћШѓЮЊzЃЈЭђдЊЃЉЃЎЃЈзЂЃКШєЩЯвЛФъгЏРћЃЌдђгЏРћВЛМЦШыЯТвЛФъЕФФъРћШѓЃЛШєЩЯвЛФъПїЫ№ЃЌдђПїЫ№МЦзїЯТвЛФъЕФГЩБОЃЎЃЉ
(ЭђМў)гыЯњЪлМлИёxЃЈдЊ/МўЃЉЕФЙиЯЕШчЭМЫљЪОЃЌЦфжаABЮЊЗДБШР§КЏЪ§ЭМЯѓЕФвЛВПЗжЃЌBCЮЊвЛДЮКЏЪ§ЭМЯѓЕФвЛВПЗжЃЎЩшЙЋЫОЯњЪлетжжЫЎОЛЛЏВњЦЗЕФФъРћШѓЮЊzЃЈЭђдЊЃЉЃЎЃЈзЂЃКШєЩЯвЛФъгЏРћЃЌдђгЏРћВЛМЦШыЯТвЛФъЕФФъРћШѓЃЛШєЩЯвЛФъПїЫ№ЃЌдђПїЫ№МЦзїЯТвЛФъЕФГЩБОЃЎЃЉ
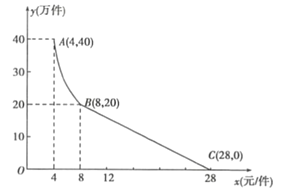
ЃЈ1ЃЉЧыЧѓГіyЃЈЭђМўЃЉгыxЃЈдЊ/МўЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЧѓГіЕквЛФъетжжЫЎОЛЛЏВњЦЗЕФФъРћШѓzЃЈЭђдЊЃЉгыxЃЈдЊ/МўЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГіЕквЛФъФъРћШѓЕФзюДѓжЕЃЛ
ЃЈ3ЃЉМйЩшЙЋЫОЕФетжжЫЎОЛЛЏВњЦЗЕквЛФъЧЁКУАДФъРћШѓzЃЈЭђдЊЃЉШЁЕУзюДѓжЕЪБНјааЯњЪлЃЌЯжИљОнЕквЛФъЕФгЏПїЧщПіЃЌОіЖЈЕкЖўФъНЋетжжЫЎОЛЛЏВњЦЗУПМўЕФЯњЪлМлИёxЃЈдЊЃЉЖЈдк8дЊвдЩЯЃЈ![]() ЃЉЃЌЕБЕкЖўФъЕФФъРћШѓВЛЕЭгк103ЭђдЊЪБЃЌЧыНсКЯФъРћШѓzЃЈЭђдЊЃЉгыЯњЪлМлИёxЃЈдЊ/МўЃЉЕФКЏЪ§ЪОвтЭМЃЌЧѓЯњЪлМлИёxЃЈдЊ/МўЃЉЕФШЁжЕЗЖЮЇЃЎ
ЃЉЃЌЕБЕкЖўФъЕФФъРћШѓВЛЕЭгк103ЭђдЊЪБЃЌЧыНсКЯФъРћШѓzЃЈЭђдЊЃЉгыЯњЪлМлИёxЃЈдЊ/МўЃЉЕФКЏЪ§ЪОвтЭМЃЌЧѓЯњЪлМлИёxЃЈдЊ/МўЃЉЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉ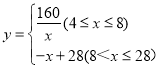 ЃЛЃЈ2ЃЉЕБ4ЁмxЁм8ЪБЃЌ
ЃЛЃЈ2ЃЉЕБ4ЁмxЁм8ЪБЃЌ![]() ЃЛЕБ8ЃМxЁм28ЪБЃЌ
ЃЛЕБ8ЃМxЁм28ЪБЃЌ![]() ЃЛЕБУПМўЕФЯњЪлМлИёЖЈ ЮЊ16дЊЪБЃЌЕквЛФъЕФФъРћШѓзюДѓЮЊ-16ЭђдЊЃЛЃЈ3ЃЉЕБ11ЁмxЁм21ЪБЃЌЕкЖўФъЕФФъРћШѓzВЛЕЭгк103ЭђдЊЃЎ
ЃЛЕБУПМўЕФЯњЪлМлИёЖЈ ЮЊ16дЊЪБЃЌЕквЛФъЕФФъРћШѓзюДѓЮЊ-16ЭђдЊЃЛЃЈ3ЃЉЕБ11ЁмxЁм21ЪБЃЌЕкЖўФъЕФФъРћШѓzВЛЕЭгк103ЭђдЊЃЎ
ЁОНтЮіЁП
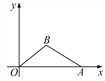
ЃЈ1ЃЉНЋЕуAЕФзјБъДњШыЗДБШР§КЏЪ§ЧѓНтМДПЩЧѓГіЗДБШР§КЏЪ§ЕФНтЮіЪНЃЌдйНЋЕуBКЭЕуCЕФзјБъДњШывЛДЮКЏЪ§ЧѓНтМДПЩЕУГівЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉИљОнЙЋЪНЁАзмРћШѓ=ЕЅМўРћШѓЁСЪ§СПЁБМДПЩЕУГіНтЮіЪНЃЌдйИљОнЖўДЮКЏЪ§ЕФаджЪМДПЩЕУГіД№АИЃЛ
ЃЈ3ЃЉЯШЧѓГіЕкЖўФъЕФФъРћШѓЙЋЪНдйСюФъРћШѓЕШгк103ЃЌНтвЛдЊЖўДЮЗНГЬВЂНсКЯЭМЯёаджЪМДПЩЕУГіД№АИЃЎ
НтЃКЃЈ1ЃЉЕБ4ЁмxЁм8ЃЌЩшy=![]() ЃЌНЋAЃЈ4ЃЌ40ЃЉДњШы
ЃЌНЋAЃЈ4ЃЌ40ЃЉДњШы
ЕУk=4ЁС40=160ЃЌ
ЫљвдyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЮЊЃКy=![]() ЃЌ
ЃЌ
ЕБ8ЃМxЁм28ЪБЃЌЩшy=kx+bЃЌ
НЋBЃЈ8ЃЌ20ЃЉЁЂCЃЈ28ЃЌ0ЃЉДњШыЕУ
![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЁрyгыxжЎМфЕФКЏЪ§ЙиЯЕЮЊy=-x+28ЃЌ
ЁрзлЩЯЫљЪіЕУЃК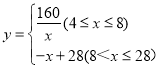 ЃЛ
ЃЛ
ЃЈ2ЃЉЕБ4ЁмxЁм8ЪБЃЌ![]() ЃЌ
ЃЌ
ЁпzЫцзХxЕФдіДѓЖјдіДѓЃЌ
ЁрЕБx=8ЪБЃЌzзюДѓжЕЮЊ-80ЃЌ
ЕБ8ЃМxЁм28ЪБЃЌ![]()
ЁрЕБx=16ЪБЃЌzзюДѓжЕЮЊ-16ЃЌ
Ёп-80ЃМ-16ЃЌ
ЁрЕБУПМўЕФЯњЪлМлИёЖЈ ЮЊ16дЊЪБЃЌЕквЛФъЕФФъРћШѓзюДѓЮЊ-16ЭђдЊЃЛ
ЃЈ3ЃЉЁпЕквЛФъЕФФъРћШѓЮЊ-16ЭђдЊЃЌ
Ёр-16ЭђдЊгІзїЮЊЕкЖўФъЕФГЩБОЃЌ
ЁрЕкЖўФъЕФФъРћШѓz=ЃЈx-4ЃЉЃЈ-x+28ЃЉ-16=![]() ЃЌ
ЃЌ
Сюz=103ЃЌдђ![]() =103ЃЌ
=103ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
дкЦНУцжБНЧзјБъЯЕжаЃЌЛГіzгыxЕФКЏЪ§ЪОвтЭМШчЭМЃЌ
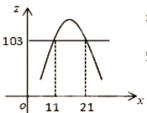
ЙлВьПЩжЊЃКzЁн103ЪБЃЌ11ЁмxЁм21ЃЌ
ЁрЕБ11ЁмxЁм21ЪБЃЌЕкЖўФъЕФФъРћШѓzВЛЕЭгк103ЭђдЊЃЎ

 ПкЫуЬтПЈМггІгУЬтМЏбЕЯЕСаД№АИ
ПкЫуЬтПЈМггІгУЬтМЏбЕЯЕСаД№АИЁОЬтФПЁПФГжабЇГѕШ§ФъМЖЛ§МЋЭЦНјзпАржЦНЬбЇЃЎЮЊСЫСЫНтвЛЖЮЪБМфвдРДЃЌЁАжСЩЦАрЁБЕФбЇЯАаЇ ЙћЃЌФъМЖзщжЏСЫЖрДЮЖЈЪБВтЪдЃЌЯжЫцЛњбЁШЁМзЁЂввСНИіЁАжСЩЦАрЁБЃЌДгжаИїГщШЁ![]() УћЭЌбЇдкФГвЛДЮЖЈЪБВтЪджаЕФЪ§бЇГЩМЈЃЌЦфНсЙћМЧТМШчЯТЃК
УћЭЌбЇдкФГвЛДЮЖЈЪБВтЪджаЕФЪ§бЇГЩМЈЃЌЦфНсЙћМЧТМШчЯТЃК
ЪеМЏЪ§ОнЃК
ЁАжСЩЦАрЁБМзАр![]() ЕФУћЭЌбЇЕФЪ§бЇГЩМЈЭГМЦЃЈТњЗжЮЊ 100 ЗжЃЉЃЈЕЅЮЛЃКЗжЃЉ
ЕФУћЭЌбЇЕФЪ§бЇГЩМЈЭГМЦЃЈТњЗжЮЊ 100 ЗжЃЉЃЈЕЅЮЛЃКЗжЃЉ
![]()
![]()
ЁАжСЩЦАрЁБввАрЕФ![]() УћЭЌбЇЕФЪ§бЇГЩМЈЭГМЦЃЈТњЗжЮЊ 100 ЗжЃЉЃЈЕЅЮЛЃКЗжЃЉ
УћЭЌбЇЕФЪ§бЇГЩМЈЭГМЦЃЈТњЗжЮЊ 100 ЗжЃЉЃЈЕЅЮЛЃКЗжЃЉ
![]()
![]()
ећРэЪ§ОнЃКЃЈГЩМЈЕУЗжгУ![]() БэЪОЃЉ
БэЪОЃЉ
ЗжЪ§ Ъ§СП АрМЖ |
|
|
|
|
|
МзАрЃЈШЫЪ§ЃЉ | 1 | 3 | 4 | 6 | 6 |
ввАрЃЈШЫЪ§ЃЉ | 1 | 1 | 8 | 6 | 4 |
ЗжЮіЪ§ОнЃЌВЂЛиД№ЯТСаЮЪЬтЃК
![]() ЭъГЩЯТБэЃК
ЭъГЩЯТБэЃК
ЦНОљЪ§ | жаЮЛЪ§ | жкЪ§ | |
МзАр |
|
|
|
ввАр |
|
|
|
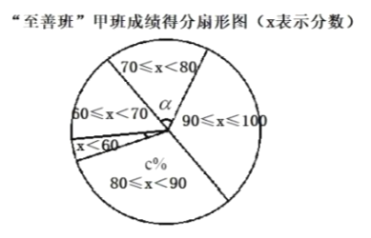
![]() дкЁАжСЩЦАрЁБМзАрЕФЩШаЮЭМжаЃЌ ГЩМЈдк
дкЁАжСЩЦАрЁБМзАрЕФЩШаЮЭМжаЃЌ ГЩМЈдк![]() ЕФЩШаЮжаЃЌЫљЖдЕФдВаФНЧ
ЕФЩШаЮжаЃЌЫљЖдЕФдВаФНЧ![]() ЕФЖШЪ§ЮЊ ЃЎ ЙРМЦШЋВПЁАжСЩЦАрЁБЕФ
ЕФЖШЪ§ЮЊ ЃЎ ЙРМЦШЋВПЁАжСЩЦАрЁБЕФ![]() ШЫжагХауШЫЪ§ЮЊ ШЫЃЎЃЈ
ШЫжагХауШЫЪ§ЮЊ ШЫЃЎЃЈ![]() ЗжМАвдЩЯЮЊгХауЃЉЃЎ
ЗжМАвдЩЯЮЊгХауЃЉЃЎ
![]() ИљОнвдЩЯЪ§ОнЃЌФуШЯЮЊЁАжСЩЦАрЁБ АрЃЈЬюЁАМзЁБЛђЁАввЁБЃЉЫљбЁШЁзібљБО ЕФЭЌбЇЕФбЇЯАаЇЙћИќКУвЛаЉЃЌФуЫљзіХаЖЯЕФРэгЩЪЧЃК
ИљОнвдЩЯЪ§ОнЃЌФуШЯЮЊЁАжСЩЦАрЁБ АрЃЈЬюЁАМзЁБЛђЁАввЁБЃЉЫљбЁШЁзібљБО ЕФЭЌбЇЕФбЇЯАаЇЙћИќКУвЛаЉЃЌФуЫљзіХаЖЯЕФРэгЩЪЧЃК
Ђй
Ђк
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌаЁРюЭЌбЇЖдИУКЏЪ§ЕФЭМЯѓгыаджЪНјааСЫЬНОПЃЌЯТУцЪЧаЁРюЭЌбЇЬНОПЕФЙ§ГЬЃЌВЙГфЭъећЃК
ЃЌаЁРюЭЌбЇЖдИУКЏЪ§ЕФЭМЯѓгыаджЪНјааСЫЬНОПЃЌЯТУцЪЧаЁРюЭЌбЇЬНОПЕФЙ§ГЬЃЌВЙГфЭъећЃК
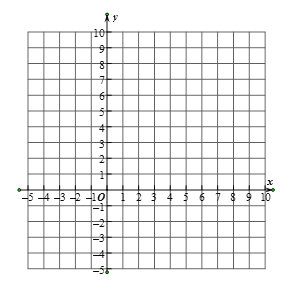
ЃЈ1ЃЉжБНгаДГіздБфСПxЕФШЁжЕЗЖЮЇЃК__________ЃЛ
ЃЈ2ЃЉЯТБэЪЧyгыxЕФМИзщЖдгІжЕЃК
x | Ё | -4 | -1 | 0 |
| 1 |
|
| 3 |
| 4 | 5 | n | Ё |
y | Ё |
| m |
| 0 | -1 | -4 | 8 | 5 | 4 |
| 3 |
| Ё |
дђm=ЁЁЁЁЃЌn=ЁЁЁЁЃЛ
ЃЈ3ЃЉШчЭМЫљЪОЃЌдкЦНУцжБНЧзјБъЯЕxoyжаЃЌУшГівдЩЯБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЌВЂИљОнУшГіЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЛ
ЃЈ4ЃЉЙлВьКЏЪ§ЭМЯѓПЩжЊЃКИУКЏЪ§ЭМЯѓЕФЖдГЦжааФЕФзјБъЪЧ______ЃЛ
ЃЈ5ЃЉЕБ![]() ЪБЃЌЙигкxЕФЗНГЬ
ЪБЃЌЙигкxЕФЗНГЬ![]() гаЪЕЪ§НтЃЌжБНгаДГіkЕФШЁжЕЗЖЮЇ_______ЃЎ
гаЪЕЪ§НтЃЌжБНгаДГіkЕФШЁжЕЗЖЮЇ_______ЃЎ