题目内容
【题目】在平面直角坐标系xOy中,⊙O的半径为r(r>0).给出如下定义:若平面上一点P到圆心O的距离d,满足![]() ,则称点P为⊙O的“随心点”.
,则称点P为⊙O的“随心点”.

(1)当⊙O的半径r=2时,A(3,0),B(0,4),C(﹣![]() ,2),D(
,2),D(![]() ,﹣
,﹣![]() )中,⊙O的“随心点”是_____;
)中,⊙O的“随心点”是_____;
(2)若点E(4,3)是⊙O的“随心点”,求⊙O的半径r的取值范围;
(3)当⊙O的半径r=2时,直线y=x+b(b≠0)与x轴交于点M,与y轴交于点N,若线段MN上存在⊙O的“随心点”,直接写出b的取值范围.
【答案】(1)A,C;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)由![]() 可求出d的范围是
可求出d的范围是![]() ,再根据各点距离O点的距离,从而判断是否在此范围内即可;
,再根据各点距离O点的距离,从而判断是否在此范围内即可;
(2)由点E的坐标求出d=5,可根据E是⊙O的“随心点”,![]() ,可求出r的范围;
,可求出r的范围;
(3)如图,a∥b∥c∥d,⊙O的半径r=2,可求出![]() ,分两种情况,当点N在y轴正半轴时,当点N在y轴负半轴时,求出答案即可.
,分两种情况,当点N在y轴正半轴时,当点N在y轴负半轴时,求出答案即可.
解:(1)∵⊙O的半径r=2,
∴![]() r=1,
r=1,![]() r=3,
r=3,
∵![]() ,
,
∴![]() ,
,
∵A(3,0),
∴OA=3,在范围内,
∴点A是⊙O的“随心点”,
∵B(0,4),
∴OB=4,而4>3,不在范围内,
∴B不是⊙O的“随心点”,
∵C(-![]() ,2),
,2),
∴OC=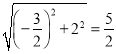 ,在范围内,
,在范围内,
∴点C是⊙O的“随心点”,
∵D(![]() ,-
,-![]() ),
),
∴OD=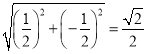 ,不在范围内,
,不在范围内,
∴点D不是⊙O的“随心点”,
故答案为:A,C
(2)∵点E(4,3),
∴OE=![]() ,即d=5,
,即d=5,
∵点E(4,3)是⊙O的“随心点”,
∴![]() ,
,
解得![]() ;
;
(3)如图a∥b∥c∥d,
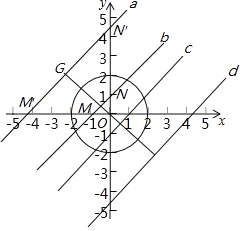
∵⊙O的半径r=2,随心点范围![]() ,
,
∴![]() ,
,
∵直线MN的解析式为y=x+b,
∴x=0时,y=b;y=0时,x=-b,
∴OM=ON,
∴直线MN与y轴夹角为45°,
①点N在y轴正半轴时,
当点M是⊙O的“随心点”,此时,点M(-1,0),
将M(-1,0)代入直线MN的解析式y=x+b中,0=-1+b,
解得,b=1,
∴b的最小值为1,
过点O作OG⊥M'N'于G,
当点G是距离⊙O最远的其中一个“随心点”时,此时OG=3,
在Rt△ON'G中,∠ON'G=45°,
∴GO=3
∴在Rt△GNN’中, ![]() ,
,
解得ON'![]() ,
,
将N'(0,![]() )代入直线MN的解析式y=x+b中,
)代入直线MN的解析式y=x+b中,![]() =b,
=b,
∴b的最大值为![]() ,
,
∴![]() ,
,
②当点N在y轴负半轴时,同①的方法得出![]() ,
,
综上所述,b的取值范围为![]() 或
或![]() .
.

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案