题目内容
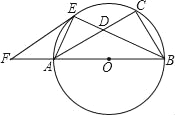
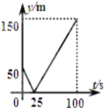
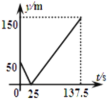
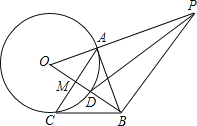
【题目】如图,点A是⊙O上一点,OA⊥AB,且OA=1,AB=![]() ,OB交⊙O于点D,作AC⊥OB,垂足为M,并交⊙O于点C,连接BC.
,OB交⊙O于点D,作AC⊥OB,垂足为M,并交⊙O于点C,连接BC.
(1)求证:BC是⊙O的切线;
(2)过点B作BP⊥OB,交OA的延长线于点P,连接PD,求sin∠BPD的值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)连结OC,根据垂径定理由AC⊥OB得AM=CM,于是可判断OB为线段AC的垂直平分线,所以BA=BC,然后利用“SSS”证明△OAB≌△OCB,得到∠OAB=∠OCB,由于∠OAB=90°,则∠OCB=90°,于是可根据切线的判定定理得BC是⊙O的切线;
(2)在Rt△OAB中,根据勾股定理计算出OB=2,根据含30度的直角三角形三边的关系得∠ABO=30°,∠AOB=60°,在Rt△PBO中,由∠BPO=30°得到PB=![]() OB=2
OB=2![]() ;在Rt△PBD中,BD=OB﹣OD=1,根据勾股定理计算出PD=
;在Rt△PBD中,BD=OB﹣OD=1,根据勾股定理计算出PD=![]() ,然后利用正弦的定义求sin∠BPD的值.
,然后利用正弦的定义求sin∠BPD的值.
解:(1)连结OC,如图,
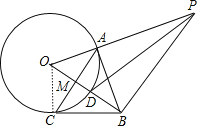
∵AC⊥OB,
∴AM=CM,
∴OB为线段AC的垂直平分线,
∴BA=BC,
在△OAB和△OCB中
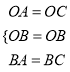 ,
,
∴△OAB≌△OCB,
∴∠OAB=∠OCB,
∵OA⊥AB,
∴∠OAB=90°,
∴∠OCB=90°,
∴OC⊥BC,
∴BC是⊙O的切线;
(2)解:在Rt△OAB中,OA=1,AB=![]() ,
,
∴![]() ,
,
∴∠ABO=30°,∠AOB=60°,
∵PB⊥OB,
∴∠PBO=90°,
在Rt△PBO中,OB=2,∠BPO=30°,
∴PB=![]() OB=2
OB=2![]() ,
,
在Rt△PBD中,BD=OB﹣OD=2﹣1=1,PB=2![]() ,
,
∴![]() ,
,
∴sin∠BPD=![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某校为了解八年级学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知![]() .
.![]() 两组发言人数的比为
两组发言人数的比为![]() ,请结合图中相关数据回答下列问题:
,请结合图中相关数据回答下列问题:
发言次数 | |
|
|
|
|
|
|
|
|
|
|
|
|
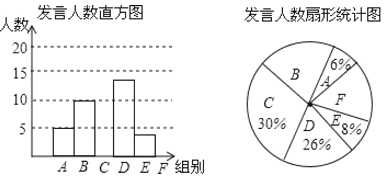
(1)求出样本容量,并补全直方图;
(2)该年级共有学生1500人,请估计全年级在这天里发言次数不少于12次的人数;
(3)已知![]() 组发言的学生中恰有1位男生,
组发言的学生中恰有1位男生,![]() 组发言的学生中有2位女生.现从
组发言的学生中有2位女生.现从![]() 组与
组与![]() 组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率
组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率
【题目】某科技公司研发出一款多型号的智能手表,一家代理商出售该公司的![]() 型智能手表,去年销售总额为80000元,今年
型智能手表,去年销售总额为80000元,今年![]() 型智能手表的售价每只比去年降了600元,若今年售出的数量与去年相同的情况下,今年的销售总额将比去年减少
型智能手表的售价每只比去年降了600元,若今年售出的数量与去年相同的情况下,今年的销售总额将比去年减少![]() .
.
(1)求今年![]() 型智能手表每只售价多少元?
型智能手表每只售价多少元?
(2)今年这家代理商准备新进一批![]() 型智能手表和
型智能手表和![]() 型智能手表共100只,它们的进货价与销售价格如下表所示,若
型智能手表共100只,它们的进货价与销售价格如下表所示,若![]() 型智能手表进货量不超过
型智能手表进货量不超过![]() 型智能手表进货量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?
型智能手表进货量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?
|
| |
进价 | 1300元/只 | 1500元/只 |
售价 | 今年的售价 | 2300元/只 |
【题目】某校为了解同学们课外阅读名著的情况,在八年级随机抽查了20名学生,调查结果如表所示:
课外名著阅读量(本) | 8 | 9 | 10 | 11 | 12 |
学生人数 | 3 | 3 | 4 | 6 | 4 |
关于这20名学生课外阅读名著的情况,下列说法错误的是( )
A.中位数是10B.平均数是10.25C.众数是11D.阅读量不低于10本的同学点70%