题目内容
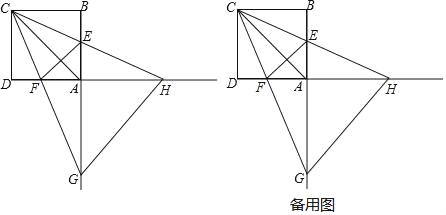
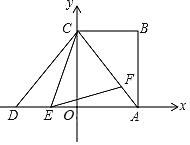
【题目】如图,矩形ABCD的顶点A、C在平面直角坐标系的坐标轴上,AB=4,CB=3,点D与点A关于y轴对称,点E、F分别是线段DA、AC上的动点(点E不与A、D重合),且∠CEF=∠ACB,若△EFC为等腰三角形,则点E的坐标为______.
【答案】(-2,0)或(![]() ,0)
,0)
【解析】
分情况讨论,根据三角形相似求解.
当△EFC为等腰三角形时,有以下三种情况:
①当CE=EF时,
∵△AEF∽△DCE,
∴△AEF≌△DCE
∴AE=CD=5,
∴OE=AE-OA=5-3=2,
∴E(-2,0);
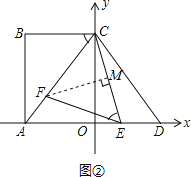
②当EF=FC时,如图②所示,过点F作FM⊥CE于M,则点M为CE中点,
∴![]()
∵△AEF∽△DCE,
∴![]()
∴![]()
解得:![]() .
.
∴![]() ,
,
∴![]()
③当CE=CF时,则有∠CFE=∠CEF,
∵∠CEF=∠ACB=∠CAO,
∴∠CFE=∠CAO,即此时F点与A点重合,这与已知条件矛盾.
综上所述,当△EFC为等腰三角形时,点E的坐标为![]()
故答案为:![]()

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目