题目内容
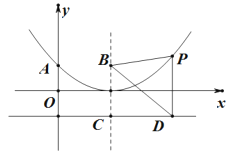
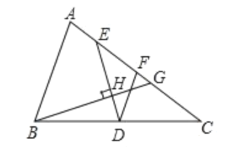
【题目】如图,在![]() 中,AB<AC,点D、F分别为BC、AC的中点,E点在边AC上,连接DE,过点B作DE的垂线交AC于点G,垂足为点H,且
中,AB<AC,点D、F分别为BC、AC的中点,E点在边AC上,连接DE,过点B作DE的垂线交AC于点G,垂足为点H,且![]() 与四边形ABDE的周长相等,设AC=b,AB=c.
与四边形ABDE的周长相等,设AC=b,AB=c.
(1)求线段CE的长度;
(2)求证:DF=EF;
(3)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)见详解;(3)
;(2)见详解;(3)![]()
【解析】
(1)根据题意得:AE+AB=CE,结合AB+AC=b+c,进而即可求解;
(2)根据中位线的性质和定义得DF =![]() c,CF=
c,CF=![]() b,结合CE=
b,结合CE=![]() ,可得EF的长,进而即可得到结论;
,可得EF的长,进而即可得到结论;
(3)连接BE、DG,设BG,DF交于点M,易得BE∥DG,从而得△ABE∽△FDG,进而得FG=![]() (bc),再证∠EGH=∠ABG,从而得AB=AG=c,结合CF=FG+CG,得到关于b,c的等式,即可得到结论.
(bc),再证∠EGH=∠ABG,从而得AB=AG=c,结合CF=FG+CG,得到关于b,c的等式,即可得到结论.
(1)∵![]() 与四边形ABDE的周长相等,点D为BC的中点,
与四边形ABDE的周长相等,点D为BC的中点,
∴AE+AB=CE,
∵AE+AB+CE=AB+AC=b+c,
∴CE=![]() =
=![]() ;
;
(2)∵点D、F分别为BC、AC的中点,
∵DF是△CAB的中位线,
∴DF=![]() AB=
AB=![]() c,AF=CF=
c,AF=CF=![]() AC=
AC=![]() b,
b,
∵CE=![]() ,
,
∴EF=CE-CF=![]()
![]() b =
b =![]() c,
c,
∴DF=EF;
(3)连接BE、DG,设BG,DF交于点M,
∵S△BDH=S△EGH,
∴S△BDG=S△DEG,
∴BE∥DG,
∴∠EBC=∠GDC,
∵DF是△CAB的中位线,
∴DF∥AB,
∴∠ABC=∠FDC,∠A=∠DFC,
∴∠ABC-∠EBC=∠FDC-∠GDC,即:∠ABE=∠FDG,
∴△ABE∽△FDG,
∴![]() ,
,
∵AE=AC-CE=b-![]() =
=![]() (bc)
(bc)
∴FG=![]() AE=
AE=![]() ×
×![]() (bc)=
(bc)=![]() (bc),
(bc),
∵DF=EF,
∴∠FED=∠FDE,
∵BG⊥DE,
∴∠FED+∠EGH=∠FDE+∠DMH=90°,
∴∠EGH=∠DMH,
又∵∠DMH=∠FMG,
∴∠EGH=∠FMG,
又∵∠FMG=∠ABG,
∴∠EGH=∠ABG,
∴AB=AG=c,
∴CG=bc,
∴CF=![]() b=FG+CG=
b=FG+CG=![]() (bc)+(bc),
(bc)+(bc),
∴3b=5c,
∴![]() =
=![]() .
.

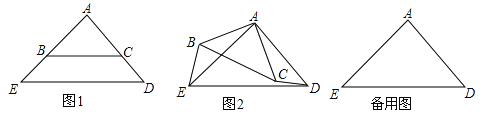
【题目】如图,正方形ABCD内部有若干个点,则用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
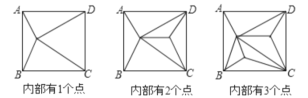
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | ... | n |
分割成三角形的个数 | 4 | 6 | _____ | _____ | ... | _____ |
(2)原正方形能否被分割成2021个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.