Question

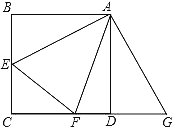
【题目】如图，正方形ABCD中，E、F分别是边BC，CD上一点，∠EAF=45°．将△ABE绕着点A逆时针旋转90°得到△ADG，连接EF，求证EF=FG．

Answer 1

【答案】证明见解析.

【解析】

首先证明FG=BE+DF；其次证明AE=AG，∠EAF=∠FAG，此为解题的关键性结论；证明△EAF≌△GAF，得到EF=FG，即可解决问题．

证明：如图，

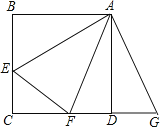
由题意得：△ABE≌△ADG，

∴∠BAE=∠DAG，AE=AG，BE=DG；

∴FG=BE+DF；

∴∠BAE+∠FAD=∠FAD+∠DAG；

∵∠EAF=45°，∠BAD=90°，

∴∠BAE+∠FAD=90°-45°=45°，

∴∠FAG=45°，∠EAF=∠FAG；

在△EAF与△GAF中，

，

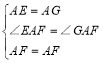∴△EAF≌△GAF（SAS），

∴EF=FG．