Question

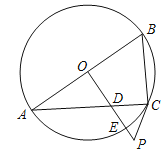
【题目】如图，抛物线过O、A、B三点，A（4,0）B（1，-3），P为抛物线上一点，过点P的直线y=x+m与对称轴交于点Q.

（1）直线PQ与x轴所夹锐角的度数，并求出抛物线的解析式.

（2）当点P在x轴下方的抛物线上时，过点C(2,2)的直线AC与直线PQ交于点D，求： PD+DQ的最大值；②PD.DQ的最大值.

Answer 1

【答案】（1）直线PQ与x轴所夹锐角的度数为45°，抛物线的解析式为y=x-4x；(2) ①PD+DQ的最大值为6;②PD·DQ的最大值为18.

【解析】

（1）根据直线的解析式求得直线PQ与x轴所夹锐角的度数，根据抛物线过O、A、B三点可求得解析式；

（2）①过点C作CH∥x轴交直线PQ于点H，可得△CHQ是等腰三角形，进而得出AD⊥PH，得出DQ=DH，从而得出PD+DQ=PH，过P点作PM⊥CH于点M，则△PMH是等腰直角三角形，得出PH=PM，因为当PM最大时，PH最大，通过求得PM的最大值，从而求得PH的最大值；

②由①可知：PD+PH≤6，设PD=a，则DQ≤6-a，得出PDDQ≤a（6-a）=-a2+6a=-（a-3）2+18，当点P在抛物线的顶点时，a=3，得出PDDQ≤18．

（1）对于直线y=x+m，

∵k=1＞0，

∴直线PQ与x轴所夹锐角的度数为45°，

∵抛物线抛物线经过点O，

∴设抛物线的解析式为y=ax+bx，把A（4,0）B（1，-3）代入得

，解得，

∴抛物线的解析式为y=x-4x.

(2) ①如图所示，过点C作CH∥x轴交直线PQ于点H，所以△CHQ是等腰三角形.

∵点A的坐标为(4,0),点C的坐标为(2,2).

∴∠ACQ=45°,

∵∠CDQ=45°+45°=90°,

∴AD⊥PH,

故DQ=DH,

∴PD+DQ=PD+DH=PH.

过点P作PM⊥CH于点M,

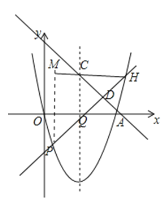
则△PMH为等腰直角三角形,

∴PH=PM,

当PM最大时,PH最大,

∴当点P在抛物线顶点处时PM取最大值,此时PM=6,

∴PH的最大值为6,即PD+DQ的最大值为6;

②由①可知PD+DQ≤6,

设PD=a,则DQ≤6-a.

设点P的坐标为(n,n-4n),

设AC/span>的解析式为y=kx+b，

将点A和点C的坐标代入得，解得，

则直线AC的解析式为y=-x+4，

如图所示，延长PM交AC于点N，

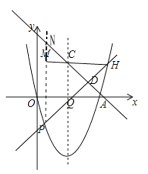
∴PD=a=PN=[4-n-（n-4n）]=-（n-3n-4）=- （n-）+ ，

又∵-<0,0<n<4,

∴当n=时,PD有最大值为,即0＜a≤.

∵PD·DQ≤a(6-a)=-a+6a=-(a-3)+18.

故当点P在抛物线的顶点时，a=3，

∵0＜3＜，

∴PDDQ的最大值为18.