题目内容
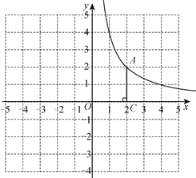
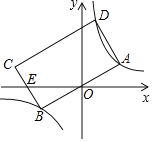
【题目】如图,抛物线![]() 与 x 轴交于点 A、B,与 y 轴交于点 C,且 OC=2OB, 点 D 为线段 OB 上一动点(不与点 B 重合),过点 D 作矩形 DEFH,点 H、F 在抛物线上,点 E 在 x 轴 上.
与 x 轴交于点 A、B,与 y 轴交于点 C,且 OC=2OB, 点 D 为线段 OB 上一动点(不与点 B 重合),过点 D 作矩形 DEFH,点 H、F 在抛物线上,点 E 在 x 轴 上.
(1)求抛物线的解析式;
(2)当矩形 DEFH 的周长最大时,求矩形 DEFH 的面积;
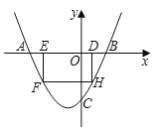
(3)在(2)的条件下,矩形 DEFH 不动,将抛物线沿着 x 轴向左平移 m 个单位,抛物线与矩形 DEFH的边交于点 M、N,连接 M、N.若 MN 恰好平分矩形 DEFH 的面积,求 m 的值.
【答案】(1)抛物线的解析式为![]() ; (2)10; (3)m的值为:
; (2)10; (3)m的值为:![]()
【解析】
(1)先求出点C的坐标,由OC=2OB,可得点B坐标,将点B坐标代入![]() 可求出a的值,即可写出抛物线的解析式;
可求出a的值,即可写出抛物线的解析式;
(2)设点D坐标为(x,0)用含x的代数式表示出矩形DEFH的周长,用函数的思想求出取其最大值时x的值,即求出点D的坐标,进一步可求出矩形DEFH的面积:
(3)如图,连接BH,EH, DF.设EH与DF交于点G,过点G作BH的平行线,交ED于M. 交HF于点N,则直线MN将矩形DEFH的面积分成相等的两半,依次求出直线BH. MN的解析式,再求出点M的坐标,即可得出m的值.
解: (1)在抛物线![]() 中,
中,
当x=0时, y=-4.
∴C (0,-4)
∴OC=4.
∵OC=2OB.
∴OB=2. .
∴B(2.0).
将B (2, 0)代入![]() ,得,
,得,![]()
∴a=![]() ;
;
∴抛物线的解析式为![]()
(2)设点D坐标为(x, 0) ,
∵四边形DEFH为矩形.
∴![]() ,
,
∵![]()
∴抛物线对称轴为x=-1,
∴点H到对称轴的距离为x+1.
由对称性可知DE=FH=2x+2,
∴矩形DEFH的周长为:![]()
∴当x=1时,矩形DEFH周长取得最大值13,
∴此时![]()
∴HF=2x+2=4. DH=![]()
∴![]()
(3)如图,连接BH, EH, DF.设EH与DF交于点G,
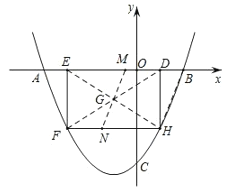
过点G作BH的平行线,交ED于M,交HF于点N,则直线MN将矩形DEFH的面积分成相等的两半,
由(2)知,抛物线对称轴为x=-1, ![]() ,
,
∴![]()
设直线BH的解析式为y=kx+b,
将点B (2. 0),![]() 代入, 得,
代入, 得,
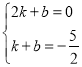
解得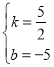
∴直线BH的解析式为![]() .
.
∴可设直线MN的解析式为![]()
将点![]() 代入,得
代入,得![]()
∴直线MN的解析式为![]()
当y=0时,![]()
∴![]()
∵B(2,0),
∴将抛物线沿着x轴向左平移![]() 个单位,抛物线与矩形DEFH的边交于点M、N,连接M、N,则MN恰好平分矩形DEFH的面积,
个单位,抛物线与矩形DEFH的边交于点M、N,连接M、N,则MN恰好平分矩形DEFH的面积,
∴m的值为:![]()

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案【题目】数学活动课上,小明同学根据学习函数的经验,对函数的图像、性质进行了探究,下面是小明同学探究过程,请补充完整:
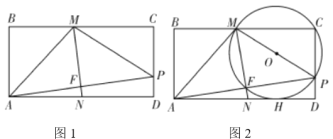
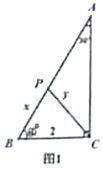
如图1,已知在![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的一个动点,连接
边上的一个动点,连接![]() .设
.设![]() ,
,![]() .
.
(初步感知)
(1)当![]() 时,则①
时,则①![]() ________,②
________,②![]() ________;
________;
(深入思考)
(2)试求![]() 与
与![]() 之间的函数关系式并写出自变量
之间的函数关系式并写出自变量![]() 的取值范围;
的取值范围;
(3)通过取点测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 0.5 | 1 | 1.5 | 2. | 2.5 | 3 | 3.5 | 4 |
| 2 | 1.8 | 1.7 | _____ | 2 | 2.3 | 2.6 | 3.0 | _____ |
(说明:补全表格时相关数值保留一位小数)
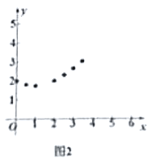
1)建立平面直角坐标系,如图2,描出已补全后的表中各对应值为坐标的点,画出该函数的图象;
2)结合画出的函数图象,写出该函数的两条性质:
①________________________________;②________________________________.
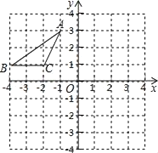
【题目】如图1,![]() ,
,![]() ,
,![]() 是郑州市二七区三个垃圾存放点,点
是郑州市二七区三个垃圾存放点,点![]() ,
,![]() 分别位于点
分别位于点![]() 的正北和正东方向,
的正北和正东方向,![]() 米.八位环卫工人分别测得的
米.八位环卫工人分别测得的![]() 长度如下表:
长度如下表:
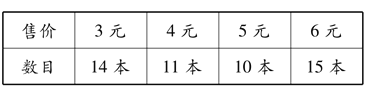
甲 | 丁 | 丙 | 丁 | 戊 | 戌 | 申 | 辰 | |
| 84 | 76 | 78 | 82 | 70 | 84 | 86 | 80 |
他们又调查了各点的垃圾量,并绘制了下列间不完整的统计图2.
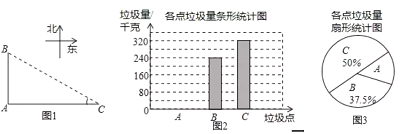
(1)表中的中位数是 、众数是 ;
(2)求表中![]() 长度的平均数
长度的平均数![]() ;
;
(3)求![]() 处的垃圾量,并将图2补充完整;
处的垃圾量,并将图2补充完整;
(4)用(2)中的![]() 作为
作为![]() 的长度,要将
的长度,要将![]() 处的垃圾沿道路
处的垃圾沿道路![]() 都运到
都运到![]() 处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.
处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.