Question

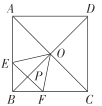
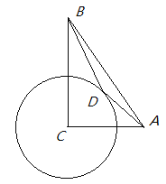
【题目】如图，A、P、B、C是⊙O上四点，∠APC=∠CPB=60°．

（1）求证：△ABC是等边三角形；

（2）连接OA，OB，当点P位于什么位置时，四边形PBOA是菱形？并说明理由；

（3）已知PA=a，PB=b，求PC的长（用含a和b的式子表示）．

Answer 1

【答案】（1）证明见解析；（2）当点P位于的中点时，四边形PBOA是菱形，理由见解析；（3）a+b．

【解析】

（1）利用圆周角定理得到∠BAC＝∠CPB＝60°，则∠ABC＝∠BAC＝∠ACB＝60°，从而可判断△ABC为等边三角形；

（2）当点P位于的中点时，四边形PBOA是菱形，连接OP，如图1，先证明∠AOP＝∠BOP＝60°，再证明△OAP和△OBP都为等边三角形，从而得到四边形PBOA是菱形；

（3）如图2，在PC上截取PD＝PA，证明△APB≌△ADC得到PB＝DC，从而得到PC＝PD＋DC＝PA＋PB＝a＋b．

（1）证明：∵∠BAC=∠CPB=60°，

∠ABC=∠APC=60°，．

∴∠ABC=∠BAC=∠ACB=60°，

∴△ABC为等边三角形；

(2)解：当点P位于的中点时，四边形PBOA是菱形．

理由如下：连接OP，

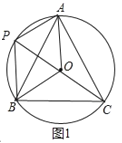
∵∠AOB=2∠ACB=120°，P是的中点，

∴∠AOP=∠BOP=60°

又∵OA=OP=OB，

∴△OAP和△OBP都为等边三角形，

∴OA=AP=OB=PB

∴四边形PBOA是菱形．

（3）解：如图2，在PC上截取PD＝PA，

又∵∠APC＝60°，

∴△APD是等边三角形，

∴PA＝DA，∠DAP＝60°，

∵∠PAB＋∠BAD＝∠BAD＋∠DAC，

∴∠PAB＝∠DAC，

在△APB和△ADC中

，

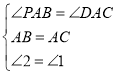∴△APB≌△ADC（ASA），

∴PB＝DC，

又∵PA＝PD，

∴PC＝PD＋DC＝PA＋PB＝a＋b．