题目内容
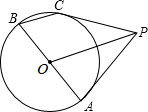
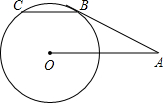
如图，PA为圆的切线，A为切点，PBC为割线，∠APC的平分线交AB于点D，交AC于点E．
求证：（1）AD=AE；（2）AB•AE=AC•DB．
求证：（1）AD=AE；（2）AB•AE=AC•DB．
证明：（1）∵∠ADE=∠APD+∠PAD，∠AED=∠CPE+∠C，
又∠APD=∠CPE，∠PAD=∠C．
∴∠ADE=∠AED．
∴AD=AE．
（2）∵∠APB=∠CPA，∠PAB=∠C，
∴△APB∽△CPA，得
=
．
∵∠APE=∠BPD，∠AED=∠ADE=∠PDB，
∴△PBD∽△PEA，得
=
．
∴
=
．
∴AB•AE=AC•DB．
又∠APD=∠CPE，∠PAD=∠C．
∴∠ADE=∠AED．
∴AD=AE．
（2）∵∠APB=∠CPA，∠PAB=∠C，
∴△APB∽△CPA，得
| AB |
| AC |
| PB |
| PA |
∵∠APE=∠BPD，∠AED=∠ADE=∠PDB，
∴△PBD∽△PEA，得
| PB |
| PA |
| DB |
| AE |
∴
| AB |
| AC |
| DB |
| AE |
∴AB•AE=AC•DB．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
相关题目
