题目内容
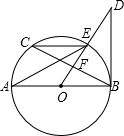
如图,PA、PB切⊙O于A、B,PO及其延长线分别交⊙O于C、D,AE为⊙O的直径,连接AB、AC,下列结论:①
=
;②∠ABP=∠DOE;③AC平分∠PAB;④∠CAB=∠BAE;其中正确的有( )

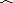 |
| CB |
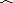 |
| DE |
| A.①②③ | B.①②③④ | C.①②④ | D.②③④ |

连接OB,如图,
由切线性质知,AO⊥PA,OB⊥PB,
∴∠AOC=∠COB,
∴
=
,
∵
=
,
∴
=
,①正确;
由题知,AB⊥OP,
又∵OA⊥AP,
∴∠PAB=∠AOP=∠DOE,②正确;
由AP为切线,
∴∠AOC=∠PAB=2∠PAC,
∴AC平分∠PAB,③正确;
④条件不足.
故选A.
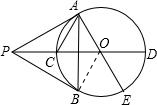
由切线性质知,AO⊥PA,OB⊥PB,
∴∠AOC=∠COB,
∴
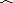 |
| BC |
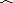 |
| AC |
∵
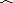 |
| AC |
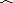 |
| DE |
∴
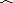 |
| CB |
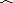 |
| DE |
由题知,AB⊥OP,
又∵OA⊥AP,
∴∠PAB=∠AOP=∠DOE,②正确;
由AP为切线,
∴∠AOC=∠PAB=2∠PAC,
∴AC平分∠PAB,③正确;
④条件不足.
故选A.


练习册系列答案
相关题目