题目内容
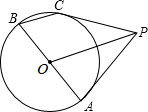
如图1,已知正方形ABCD的边长为2
,点M是AD的中点,P是线段MD上的一动点(P不与M,D重合),以AB为直径作⊙O,过点P作⊙O的切线交BC于点F,切点为E.
(1)除正方形ABCD的四边和⊙O中的半径外,图中还有哪些相等的线段(不能添加字母和辅助线);
(2)求四边形CDPF的周长;
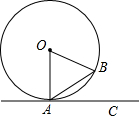
(3)延长CD,FP相交于点G,如图2所示.是否存在点P,使BF•FG=CF•OF?如果存在,试求此时AP的长;如果不存在,请说明理由.

| 3 |
(1)除正方形ABCD的四边和⊙O中的半径外,图中还有哪些相等的线段(不能添加字母和辅助线);
(2)求四边形CDPF的周长;
(3)延长CD,FP相交于点G,如图2所示.是否存在点P,使BF•FG=CF•OF?如果存在,试求此时AP的长;如果不存在,请说明理由.

(1)FB=FE,PE=PA.
(2)四边形CDPF的周长为
FC+CD+DP+PE+EF=FC+CD+DP+PA+BF
=BF+FC+CD+DP+PA
=BC+CD+DA
=2
×3=6
.
(3)存在.
∵BF•FG=CF•OF
∴
=
∵cos∠OFB=
,cos∠GFC=
∴∠OFB=∠GFC
∵∠OFB=∠OFE
∴∠OFE=∠OFB=∠GFC=60°
∴在Rt△OFB中,FE=FB=
=1
∴在Rt△GFC中
∵CG=CF•tan∠GFC=CF•tan60°=(2
-1)tan60°=6-
∴DG=CG-CD=6-3
∴DP=DG•tan∠PGD=DG•tan30°=2
-3
∴AP=AD-DP=2
-(2
-3)=3.
(2)四边形CDPF的周长为
FC+CD+DP+PE+EF=FC+CD+DP+PA+BF
=BF+FC+CD+DP+PA
=BC+CD+DA
=2
| 3 |
| 3 |
(3)存在.
∵BF•FG=CF•OF
∴
| BF |
| OF |
| CF |
| FG |
∵cos∠OFB=
| BF |
| OF |
| CF |
| FG |
∴∠OFB=∠GFC
∵∠OFB=∠OFE
∴∠OFE=∠OFB=∠GFC=60°
∴在Rt△OFB中,FE=FB=
| OB |
| tan60° |
∴在Rt△GFC中
∵CG=CF•tan∠GFC=CF•tan60°=(2
| 3 |
| 3 |
∴DG=CG-CD=6-3
| 3 |
∴DP=DG•tan∠PGD=DG•tan30°=2
| 3 |
∴AP=AD-DP=2
| 3 |
| 3 |

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目