题目内容
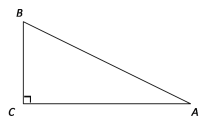
【题目】如图,△ABC 和△CDE 都是等腰直角三角形,∠ACB=∠ECD=90°,D 为 AB 边上一点.如下结论:

①△ACE≌△BCD; ②△ADE 是直角三角形; ③AD2+BD2=2CD2; ④AE=AC, 其中正确的结论有( )
A.①③④B.①②③C.①②D.①③
【答案】B
【解析】
由△ABC 和△CDE是等腰直角三角形,则BC=AC,CE=CD,由∠ACB=∠ECD=90°,得到∠ACE=∠BCD,则△ACE≌△BCD;则∠CAE=∠B=45°,则得到∠EAD=90°;由AE=BD,则AD2+BD2= AD2+AE2=ED2,由ED2=CD2+CE2=2CD2;无法证明AE=AC,即可得到答案.
解:∵△ABC 和△CDE是等腰直角三角形,
∴BC=AC,CE=CD,∠B=∠CAB=45°,
∵∠ACB=∠ECD=90°,
∴∠ACE+∠ACD=∠BCD+∠ACD=90°,
∴∠ACE=∠BCD,
∴△ACE≌△BCD;故①正确;
∴∠CAE=∠B=45°,
∴∠CAE+∠CAB=90°,
∴∠EAD=90°,
∴△ADE是直角三角形;故②正确;
在直角三角形ADE中,AD2+AE2=ED2,
∵△ACE≌△BCD,
∴AE=BD,
∴AD2+BD2= ED2,
∵ED2=CD2+CE2=2CD2,
∴AD2+BD2=2CD2;故③正确;
无法正确AE=AC;故④错误;
∴正确的有:①②③;
故选择:B.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目