题目内容
【题目】如图,在△ABC中,∠C=90°
(1)尺规作图:作AC的垂直平分线,垂足为E,交AB于点D.(不写作法,保留作图痕迹,不证明)
(2)连结CD,求证: ![]()
【答案】(1)见详解;(2)见详解.
【解析】
(1)分别以A、C为圆心,大于AC的一半为半径画弧,两弧相交与点M、N,连接MN,与AC相交与点E,与AB相交于点D,则MN为所求;
(2)由垂直平分线性质,得到CD=AD,由BC∥DE,点E为AC中点,则点D为AB中点,则AD=BD=CD,即可得到![]() .
.
解:(1)如图所示,MN是AC的垂直平分线;
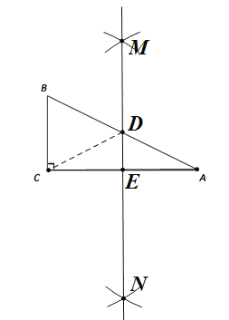
(2)由(1)知,MN是AC的垂直平分线,
∴AD=CD,BC∥DE,
∵点E是AC的中点,
∴点D是AB的中点,
∴AD=BD,
∴AD=BD=CD,
∴![]() .
.

练习册系列答案
相关题目






