题目内容
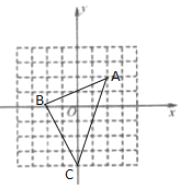
【题目】如图，每个小方格的边长为1，已知点A(2，2)，把点A先向左平移4个单位，再向下平移2个单位到达点B；把点B先向右平移2个单位，再向下平移4个单位到达点C.
(1)在图中画出△ABC，并直接写出B，C两点的坐标：B( )，C( ).
(2)求△ABC的面积.
(3)判断△ABC的形状，并说明理由.
【答案】(1)画图见解析；B(-2，0)，C(0，-4)；(2)S△ABC=10；(3)△ABC是等腰直角三角形，理由见解析.
【解析】
(1)在平面直角坐标系中画出点A，再根据点的坐标的平移方法确定出点B，C的位置，然后顺次连接即可；
(2)将△ABC放在边长为4和6的矩形中，利用矩形的面积减去三个直角三角形的面积，即可求出△ABC的面积；
(3)利用勾股定理求出AB2、BC2、AC2，可得AB2+BC2=AC2，AB=BC，即可得到△ABC的形状.
解：(1)如图，B(-2，0)，C(0，-4)；
(2) S△ABC=4×6-
×2×4-×2×6-×2×4=24-4-6-4=10；
(3)∵AB2=22+42=20，BC2=22+42=20，AC2=22+62=40，
∴AB2+BC2=AC2，AB=BC，
∴△ABC是等腰直角三角形.
练习册系列答案
中考解读考点精练系列答案
相关题目
