Question

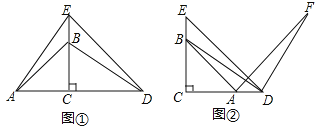
【题目】如图①，点P是∠AOB的平分线OC上的一点，我们可以分别OA、OB在截取点M、N，使OM=ON，连结PM、PN，就可得到.

（1）请你在图①中,根据题意，画出上面叙述的全等三角形和，并加以证明．

（2）请你参考（1）中的作全等三角形的方法，解答下列问题：

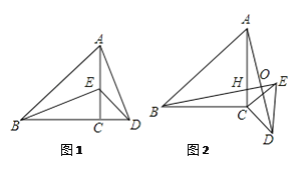
（Ⅰ）如图②，在△ABC中，∠ACB是直角,∠B=60°，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F．请你判断并写出FE与FD之间的数量关系.

（Ⅱ）如图③，在△ABC中，如果∠ACB不是直角，而（1）中的其它条件不变，请问，你在（Ⅰ）中所得结论是否仍然成立？若成立，请证明；若不成立，请说明理由．

Answer 1

【答案】（1）见详解；（2）（Ⅰ）FE=FD，证明见详解；（Ⅱ）FE=FD仍成立；理由见详解.

【解析】

（1）根据题意，画出图形，直接根据SAS，即可证明；

（2）（Ⅰ）过点F作FG⊥AB，FH⊥BC，垂足分别为G、H，连接BF，由角平分线性质，得到FG=FH，∠FGE=∠FHD=90°，又∠FDH=FEG=75°，由AAS证明△EFG≌△DFH，即可得到FE=FD；

（Ⅱ）与（Ⅰ）同理，得到FG=FH，∠FGE=∠FHD=90°，由∠ABC=60°，得到∠FDH=∠ABC+∠BAF=60°+∠BAF，又∠FEG =∠BAF+60°，则∠FDH=∠FEG=∠BAF+60°，然后利用AAS证明△EFG≌△DFH，即可得到结论成立.

解：（1）如图，

∵OC是∠AOB的平分线，

∴∠AOC=∠BOC，

∵OM=ON，OP=OP，

∴△POM≌△PON（SAS）；

（2）（Ⅰ）如图，过点F作FG⊥AB，FH⊥BC，垂足分别为G、H，连接BF，

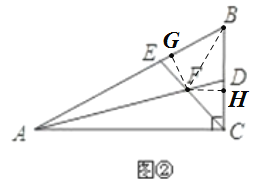
∵AD平分∠BAC，CE平分∠ACB，

∴点F为内心，则BF平分∠ABC，

∵FG⊥AB，FH⊥BC，

∴FG=FH，∠FGE=∠FHD=90°，

∵∠B=60°，∠ACB=90°，

∴∠BAC=30°，

∵AD平分∠BAC，CE平分∠ACB，

∴∠DAC=15°，∠ACE=45°，

∴∠FEG=∠BAC+ACE=30°+45°=75°，∠FDH=90°-15°=75°，

∴∠FDH=FEG=75°，

∴△EFG≌△DFH（AAS），

∴FE=FD；

（Ⅱ）FE=FD仍成立；理由如下：

如图，与（Ⅰ）同理，过点F作FG⊥AB，FH⊥BC，垂足分别为G、H，连接BF，

由（Ⅰ）可知，FG=FH，∠FGE=∠FHD=90°，

∵∠ABC=60°，

∴∠BAC+∠BCA=120°，

∵AD平分∠BAC，CE平分∠ACB，

∴∠FAC+∠FCA=（∠BAC+∠BCA）=，

∵∠FDH=∠ABC+∠BAF=60°+∠BAF，

∠FEG=∠BAC+∠FCA=∠BAF+∠FAC+∠FCA=∠BAF+60°，

∴∠FDH=∠FEG=∠BAF+60°，

∴△EFG≌△DFH（AAS），

∴FE=FD.