题目内容
【题目】探究并解决问题:
探究
倍延三角形的一条中线,我们可以发现一些有用的结论.
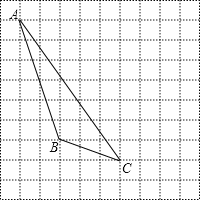
已知,如图①所示,AD为△ABC的中线,延长AD到E,使AD=DE,连接BE、CE.
(1)求证:AB∥CE.

(2)请再写出两条不同类型的结论.
解决问题
如图所示②,分别以△ABC的边AB和AC为边,向三角形的外侧作两个等腰直角三角形,AB=AD,AC=AE,∠BAD = ∠CAE=90°,点M为BC的中点,连接DE,AM,试问线段AM、DE之间存在什么关系?并说明理由.
【答案】探究(1)见解析;(2)见解析;解决问题:ED=2AM,AM⊥ED;证明见解析.
【解析】
探究(1)先证明四边形BEAC是平行四边形,即可完成;(2)根据(1)所得的平行四边形,写两条性质即可;解决问题:ED=2AM,AM⊥ED.延长AM到G,使MG=AM,连BG,则ABGC是平行四边形,再结合已知条件可以证明△DAE≌△ABG,根据全等三角形的性质可以得到DE=2AM,∠BAG=∠EDA,再延长MG交DE于H,因为∠B4G+∠DAH=90°,所以∠HDA+∠DAH=90°这样就证明了AMLED;
解:探究(1)∵AD为△ABC的中线,
∴BD=DC
又∵AD=DE
∴四边形ABEC是平行四边形
∴AB∥CE
(2)∵四边形ABEC是平行四边形
∴BE=AC,BE∥AC,∠BAC=∠BEC等写两个即可.
解决问题:
ED=2AM,AM⊥ED
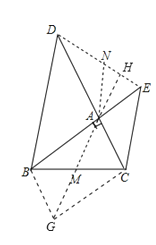
证明:延长AM到G,使MG=AM,连BG,则ABGC是平行四边形,再延长M4交DE于H.
∴AC=BG,∠ABG+∠BAC=180°
又∵∠DAE+∠BAC=180°,
∴∠ABG=∠DAE.
∴△DAE≌△ABG
∴DE=2AM,∠BAG=∠EDA.
延长MA交DE于H,
∵∠BAG+∠DAH=90°,
∴∠HDA+∠DAH=90°.
AM⊥ED.