题目内容
【题目】在平面直角坐标系中,点A(m,n)在第一象限内,m,n均为整数,且满足![]() .
.
(1)求点A的坐标;
(2)将线段OA向下平移a(a>0)个单位后得到线段![]() ,过点
,过点![]() 作
作![]() 轴于点B,若
轴于点B,若![]() ,求a的值;
,求a的值;
(3)过点A向x轴作垂线,垂足为点C,点M从O出发,沿y轴的正半轴以每秒2个单位长度的速度运动,点N从点C出发,以每秒3个单位长度的速度向x轴负方向运动,点M与点N同时出发,设点M的运动时间为t秒,当![]() 时,判断四边形AMON的面积
时,判断四边形AMON的面积![]() 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.
【答案】(1)点A的坐标为(3,2);(2)![]() ;(3)四边形AMON的面积是定值3,理由见解析
;(3)四边形AMON的面积是定值3,理由见解析
【解析】
(1)根据题意求出n的解集,即可解答
(2)根据题意可分期款讨论:当点B在原点O的上方时,![]() ;当点B在原点O的下方时,
;当点B在原点O的下方时,![]()
(3)过点A向y轴作垂线,垂足为A`,得到C(3,0),m(0,2t),n(3-3t),A`(0,2)
,再利用![]() ,即可解答
,即可解答
(1)∵![]()
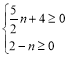
解之,得![]()
∵![]() ,且n为正整数
,且n为正整数
∴![]()
又∵m为正整数
∴n=2,m=3
故点A的坐标为(3,2)
(2)平移后:![]()
当点B在原点O的上方,如图1:
∵![]()
∴(2-a)-(-a)=3(2-a)
∴![]()
当点B在原点O的下方,如图2:
∵![]()
∴(2-a)-(-a)=3(2-a)
∴![]()
故![]()
(3)如图3,过点A向y轴作垂线,垂足为A`,则
C(3,0),m(0,2t),n(3-3t),A`(0,2)
![]()
=2![]()
=6-3-3t+3t
=3
故四边形AMON的面积是定值3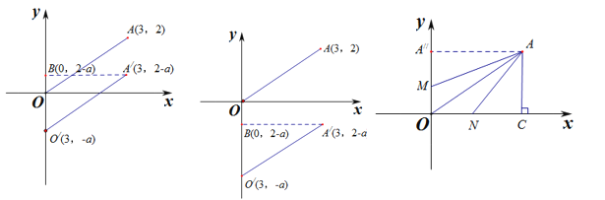

练习册系列答案
相关题目