题目内容
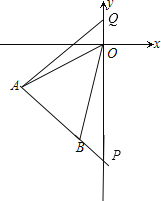
【题目】如图,平面直角坐标系中,A(﹣3,﹣2)、B(﹣1,﹣4)
(1)直接写出:S△OAB= ;
(2)延长AB交y轴于P点,求P点坐标;
(3)Q点在y轴上,以A、B、O、Q为顶点的四边形面积为6,求Q点坐标.

【答案】(1)5;(2)(0,﹣5);(3) (0, ![]() )或(0,﹣2).
)或(0,﹣2).
【解析】试题解析:(1)延长AB交y轴于P点,如图,利用待定系数法求出直线AB的解析式为y=-x-5,则得到P(0,-5),然后根据三角形面积公式和利用S△OAB=S△AOP-S△OBP进行计算即可;
(2)由(1)得到P点的坐标;
(3)分类讨论:当Q在y轴的正半轴上时,利用S四边形ABOQ=S△AOB+S△AOQ得到S△AOQ=1,再根据三角形面积公式求出OQ.从而得到Q点坐标;当Q在y轴的负半轴上时,利用S四边形ABOQ=S△AOB+S△BOQ得到S△BOQ=1,再根据三角形面积公式求出OQ.从而得到Q点坐标.
试题解析:(1)延长AB交y轴于P点,如图,
设直线AB的解析式为y=kx+b,
把A(﹣3,﹣2)、B(﹣1,﹣4)代入得![]()
解得![]() .
.
所以直线AB的解析式为y=﹣x﹣5,
当x=0时,y=﹣x﹣5=﹣5,则P(0,﹣5),
所以S△OAB=S△AOP﹣S△OBP
=![]() ×5×3﹣
×5×3﹣![]() ×5×1
×5×1
=5.
(2)由(1)得到P点的坐标为(0,﹣5);
(3)当Q在y轴的正半轴上时,∵S四边形ABOQ=S△AOB+S△AOQ,
∴S△AOQ=6﹣5=1,
∴![]() ×3×OQ=1,
×3×OQ=1,
解得OQ=![]() .
.
则此时Q点的坐标为(0, ![]() );
);
当Q在y轴的负半轴上时,
∵S四边形ABOQ=S△AOB+S△BOQ,
∴S△BOQ=1,
∴S△AOQ=6﹣5=1,
∴![]() ×1×OQ=1,
×1×OQ=1,
解得OQ=2,
则此时Q点的坐标为(0,﹣2),
即Q点坐标为(0, ![]() )或(0,﹣2).
)或(0,﹣2).