[题目]如图.要证明平行四边形ABCD为正方形.那么我们需要在四边形ABCD是平行四边形的基础上.进一步证明( )A.AB=AD且AC⊥BDB.AB=AD且AC=BDC.∠A=∠B且AC=BDD.AC和BD互相垂直平分题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，要证明平行四边形ABCD为正方形，那么我们需要在四边形ABCD是平行四边形的基础上，进一步证明（）

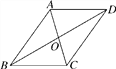
A.AB=AD且AC⊥BDB.AB=AD且AC=BDC.∠A=∠B且AC=BDD.AC和BD互相垂直平分

【答案】B

【解析】

解：A．根据有一组邻边相等的平行四边形是菱形，或者对角线互相垂直的平行四边形是菱形，所以不能判断平行四边形ABCD是正方形；

B．根据邻边相等的平行四边形是菱形，对角线相等的平行四边形为矩形，所以能判断四边形ABCD是正方形；

C．根据一组邻角相等的平行四边形是矩形，对角线相等的平行四边形也是矩形，即只能证明四边形ABCD是矩形，不能判断四边形ABCD是正方形；

D．根据对角线互相垂直的平行四边形是菱形，对角线互相平分的四边形是平行四边形，所以不能判断四边形ABCD是正方形．

故选B．

练习册系列答案

相关题目

【题目】定义：若两个函数y1和y2的自变量x的取值范围相同，我们不妨把y1和y2的比值y称为x的比函数，且比函数的自变量x的取值范围不发生改变．例如：y1＝x2+2x（x＞0），y2＝x（x＞0），则x的比函数为y＝＝x+2（x＞0）．

（1）已知y1＝x2﹣4（2≤x≤3），y2＝x+2（2≤x≤3），写出x的比函数y的解析式，并求出y的取值范围；

（2）已知y1＝x+2（x＞1），y2＝x﹣2（x＞1），求x的比函数y的图象上的整数点（横坐标和纵坐标都为整数的点）的坐标；

（3）已知y1＝x2﹣x+1，y2＝x2+x+1，若x的比函数y的图象与抛物线y3＝x2+2x+k（k为常数）存在交点，求k的取值范围．

【题目】已知二次函数y＝ax（x﹣3）+c（a＜0，0≤x≤3），反比例函数y＝（x＞0，k＞0）图象如图1所示，反比例函数y＝（x＞0，k＞0）的图象经过点P（m，n），PM⊥x轴，垂足为M，PN⊥y轴，垂足为N；且OMON＝12．

（1）求k的值；

（2）当c＝0时，计算抛物线与x轴的两个交点之间的距离．

（3）确定二次函数y＝ax（x﹣3）+c（a＜0，0≤x≤3）对称轴．

（4）如图2，当a＝﹣1时，抛物线y＝ax（x﹣3）+c（a＜0；0≤x≤3）有一时刻恰好经过P点，且此时抛物线与双曲线y＝（x＞0，k＞0）有且只有一个公共点P（如图2所示），我们不妨把此时刻的c记作c1，请直接写出抛物线y＝ax（x﹣3）+c（a＜0，0≤x≤3）的图象与双曲线y＝（x＞0，k＞0）的图象有一个公共点时c的取值范围．（温馨提示：c1作为已知数，可直接应用哦!）

【题目】有两个全等的含30°角的直角三角板重叠在一起，如图，将△A′B′C′绕AC的中点M转动，斜边A′B′刚好过△ABC的直角顶点C，且与△ABC的斜边AB交于点N，连接AA′、C′C、AC′．若AC的长为2，有以下五个结论：①AA′=1；②C′C⊥A′B′；③点N是边AB的中点；④四边形AA′CC′为矩形；⑤A′N=B′C=，其中正确的有（　　）