Question

【题目】如图，反比例函数的图象与正比例函数的图象交于点，且点的横坐标为2.

（1）求反比例函数的表达；

（2）若射线上有点，，过点作与轴垂直，垂足为点，交反比例函数图象于点，连接，，请求出的面积.

Answer 1

【答案】（1）y=(x>0)；（2）△OAB的面积为8.

【解析】

（1）将A点的横坐标代入正比例函数，可求出A点坐标，再将A点坐标代入反比例函数求出k，即可得解析式；

（2）过A点作AN⊥OM，垂足为点N，则AN∥PM，根据平行线分线段成比例得，进而求出M点坐标，将M点的横坐标分别代入反比例函数和正比例函数，求出B、P的坐标，再利用三角形面积公式求出△POM、△BOM的面积，作差得到△BOP的面积，最后根据S△OAB∶S△BAP=OA∶AP=1∶2即可求解．

解：（1）A点在正比例函数y=x的图象上，当x=2时，y=3，

∴点A的坐标为(2,3)

将(2,3)代入反比例函数解析式y= (x>0)，得，解得k=6．

∴反比例函数的表达式为y=(x>0)

（2）如图，过A点作AN⊥OM，垂足为点N，则AN∥PM，

∴.

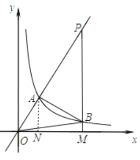
∵PA=2OA，

∴MN=2ON=4，

∴OM=ON+MN=2+4=6

∴M点的坐标为(6,0)

将x=6代入y=，得y==1，

∴点B的坐标为(6,1)

将x=6代入y=x，得y==9，

∴点P的坐标为(6,9)．

∴S△POM=×6×9=27，S△BOM=×6×1=3

∴S△BOP=27-3=24

又∵S△OAB∶S△BAP=OA∶AP=1∶2

∴S△OAB=×24=8

答：△OAB的面积为8．