Question

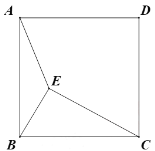
【题目】如图，已知正方ABCD内一动点E到A、B、C三点的距离之和的最小值为，则这个正方形的边长为_____________

Answer 1

【答案】

【解析】

将△ABE绕点A旋转60°至△AGF的位置，根据旋转的性质可证△AEF和△ABG为等边三角形，即可证明EF=AE,GF=BE,所以根据两点之间线段最短EA+EB+EC=GF+EF+EC≥GC，表示Rt△GMC的三边，根据勾股定理即可求出正方形的边长.

解：如图，将△ABE绕点A旋转60°至△AGF的位置，连接EF,GC,BG，过点G作BC 的垂线交CB的延长线于点M.设正方形的边长为2m，

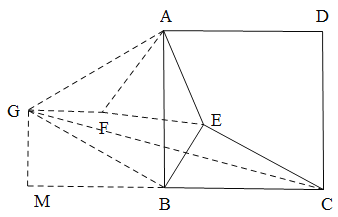
∵四边形ABCD为正方形，

∴AB=BC=2m,∠ABC=∠ABM=90°，

∵△ABE绕点A旋转60°至△AGF，

∴,

∴△AEF和△ABG为等边三角形，

∴AE=EF,∠ABG=60°，

∴EA+EB+EC=GF+EF+EC≥GC，

∴GC=，

∵∠GBM=90°-∠ABG =30°，

∴在Rt△BGM中，GM=m，BM=，

Rt△GMC中，勾股可得，

即：，

解得：，

∴边长为.

故答案为：.