��Ŀ����
����Ŀ�����壺����������y1��y2���Ա���x��ȡֵ��Χ��ͬ�����Dz�����y1��y2�ı�ֵy��Ϊx�ıȺ������ұȺ������Ա���x��ȡֵ��Χ�������ı䣮���磺y1��x2+2x��x��0����y2��x��x��0������x�ıȺ���Ϊy��![]() ��x+2��x��0����
��x+2��x��0����
��1����֪y1��x2��4��2��x��3����y2��x+2��2��x��3����д��x�ıȺ���y�Ľ���ʽ�������y��ȡֵ��Χ��
��2����֪y1��x+2��x��1����y2��x��2��x��1������x�ıȺ���y��ͼ���ϵ������㣨������������궼Ϊ�����ĵ㣩�����ꣻ
��3����֪y1��x2��x+1��y2��x2+x+1����x�ıȺ���y��ͼ����������y3��x2+2x+k��kΪ���������ڽ��㣬��k��ȡֵ��Χ��
���𰸡���1��y��x��2��0��y��1����2�������������Ϊ��3��5������4��3������6��2������3����k��4ʱ��x�ıȺ���y��ͼ����������y3��x2+2x+k��kΪ���������ڽ��㣮
��������
��1�����ݱȺ����Ķ��弴�ɵó��𰸣�
��2���ȸ��ݱȺ����Ķ���д��x�ıȺ������ٽ��Ⱥ��������һ����������һ����ʽ����ʽ�����ɵó��𰸣�
��3���ȸ��ݱȺ����Ķ���д��x�ıȺ�����������Ⱥ���y��ȡֵ��Χ��������x�ıȺ���y��ͼ����������y3��x2+2x+k��kΪ���������ڽ������ó�x2+2x+k��ȡֵ��Χ�����ɵó���.
�⣺��1��x�ıȺ���Ϊy��![]() ��
��
��2��x��3��
��0��y��1��
��2��x�ıȺ���Ϊy��![]() ��
��
��x��1��
��x��3ʱ��y��5��x��4ʱ��y��3��x��6ʱ��y��2��
��x�ıȺ���ͼ���ϵ������������Ϊ��3��5������4��3������6��2����
��3��x�ıȺ���Ϊy��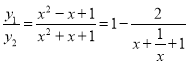 ��
��
��x��0ʱ��x+��2��
��![]() ��y��1��
��y��1��
��x��0ʱ��x+![]() ����2��
����2��
��1��y��3��
��![]() ��y��3��y��1��
��y��3��y��1��
��x�ıȺ���y��ͼ����������y3��x2+2x+k��kΪ���������ڽ��㣬
��x2+2x+k��3��
�ߵ�x����1ʱ�������ߵ���СֵΪk��1��
��k��1��3����k��4��
�൱k��4ʱ��x�ıȺ���y��ͼ����������y3��x2+2x+k��kΪ���������ڽ��㣮