Question

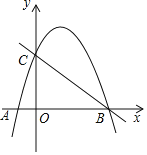
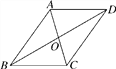
【题目】已知二次函数y＝ax（x﹣3）+c（a＜0，0≤x≤3），反比例函数y＝（x＞0，k＞0）图象如图1所示，反比例函数y＝（x＞0，k＞0）的图象经过点P（m，n），PM⊥x轴，垂足为M，PN⊥y轴，垂足为N；且OMON＝12．

（1）求k的值；

（2）当c＝0时，计算抛物线与x轴的两个交点之间的距离．

（3）确定二次函数y＝ax（x﹣3）+c（a＜0，0≤x≤3）对称轴．

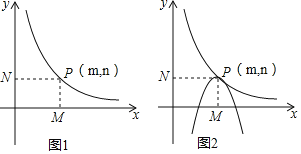
（4）如图2，当a＝﹣1时，抛物线y＝ax（x﹣3）+c（a＜0；0≤x≤3）有一时刻恰好经过P点，且此时抛物线与双曲线y＝（x＞0，k＞0）有且只有一个公共点P（如图2所示），我们不妨把此时刻的c记作c1，请直接写出抛物线y＝ax（x﹣3）+c（a＜0，0≤x≤3）的图象与双曲线y＝（x＞0，k＞0）的图象有一个公共点时c的取值范围．（温馨提示：c1作为已知数，可直接应用哦!）

Answer 1

【答案】（1）12；（2）3；（3）对称轴为x＝；（4）c＞4或c＝c1．

【解析】

（1）点P（m，n）在反比例函数y＝上，OMON＝12，k＝12；

（2）当c＝0时，y＝ax（x﹣3），函数与x轴两个交点为（0，0），（3，0）；

（3）y＝ax（x﹣3）+c＝ax2﹣3ax+c，函数的对称轴为x＝；

（4）当x＝3时c＝＝4，c＞4时，抛物线与反比例函数有一个交点，当c＝c1时，抛物线与反比例函数有一个交点.

解：（1）∵点P（m，n）在反比例函数y＝上，OMON＝12，

∴mn＝12，

∴k＝12；

（2）当c＝0时，y＝ax（x﹣3），

∴函数与x轴两个交点为（0，0），（3，0），

∴两个交点间距离为3；

（3）y＝ax（x﹣3）+c＝ax2﹣3ax+c，

∴x＝，

∴函数的对称轴为x＝；

（4）∵a＝﹣1，

∴y＝﹣x（x﹣3）+c，

当x＝3时c＝＝4，

∴c＞4时，抛物线与反比例函数有一个交点，

当c＝c1时，抛物线与反比例函数有一个交点，

综上所述：抛物线与反比例函数有一个交点时，c＞4或c＝c1．