题目内容
已知：如图，AB是⊙O的直径，点C是⊙O上的一点，CD交AB的延长线于D，∠DCB=∠CAB．
（1）求证：CD为⊙O的切线．
（2）若CD=4，BD=2，求⊙O的半径长．
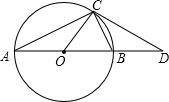
（1）求证：CD为⊙O的切线．
（2）若CD=4，BD=2，求⊙O的半径长．
（1）证明：∵∠DCB=∠CAB，∠CAB=∠ACO，
∴∠DCB=∠ACO，
∵AB是⊙O的直径，
∴∠ACB=90°，
即∠ACO+∠OCB=90°
∴∠DCB+∠OCB=90°，
∴∠OCD=90°
∴CD为⊙O的切线；
（2）设⊙O的半径为R，则OD=R+2，
∵CD=4，BD=2，∠OCD=90°，
由勾股定理得R2+42=（R+2）2，
解得：R=3，
∴⊙O的半径长为3．
∴∠DCB=∠ACO，
∵AB是⊙O的直径，
∴∠ACB=90°，
即∠ACO+∠OCB=90°
∴∠DCB+∠OCB=90°，
∴∠OCD=90°
∴CD为⊙O的切线；
（2）设⊙O的半径为R，则OD=R+2，
∵CD=4，BD=2，∠OCD=90°，
由勾股定理得R2+42=（R+2）2，
解得：R=3，
∴⊙O的半径长为3．
练习册系列答案
相关题目
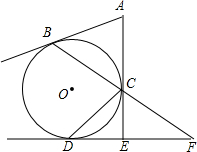DE于点F．若BC=24，sin∠F=
沿BC方向运动．设运动的时间为t（0≤t≤2），连接MN，当t为何值时△BMN为直角三角形？并求此时该三角形的面积？
