题目内容
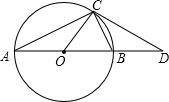
如图,已知:△ABC内接于⊙O,点D在OC的延长线上,∠B=∠D=30°.
(1)判断AD与⊙O的位置关系,并说明理由;
(2)若AC=16,求AD的长.

(1)判断AD与⊙O的位置关系,并说明理由;
(2)若AC=16,求AD的长.

(1)AD与圆O相切,理由为:
连接OA,
∵圆周角∠B与圆心角∠O都对弧AC,∠B=∠D=30°,
∴∠O=2∠B=60°,
在△ADO中,∠O=60°,∠D=30°,
∴∠DAO=90°,
∴OA⊥AD,又OA为圆的半径,
则AD与圆O相切;
(2)∵OC=OA,且∠O=60°,
∴△AOC为等边三角形,
∴OA=AC=16,
在Rt△ADO中,tanO=tan60°=
,即
=
,
则AD=16
.

连接OA,
∵圆周角∠B与圆心角∠O都对弧AC,∠B=∠D=30°,
∴∠O=2∠B=60°,
在△ADO中,∠O=60°,∠D=30°,
∴∠DAO=90°,
∴OA⊥AD,又OA为圆的半径,
则AD与圆O相切;
(2)∵OC=OA,且∠O=60°,
∴△AOC为等边三角形,
∴OA=AC=16,
在Rt△ADO中,tanO=tan60°=
| AD |
| OA |
| AD |
| 16 |
| 3 |
则AD=16
| 3 |


练习册系列答案
相关题目





 ,交AY于点D.
,交AY于点D.
