Question

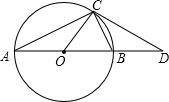
如图，⊙O是△ABC的外接圆，∠A=30°，AB是⊙O的直径，过点C作⊙O的切线，交AB延长线于D，CD=3

3

cm，
（1）求⊙O的直径；
（2）若动点M以3cm/s的速度从点A出发沿AB方向运动，同时点N以1.5cm/s的速度从B点出发沿BC方向运动．设运动的时间为t（0≤t≤2），连接MN，当t为何值时△BMN为直角三角形？并求此时该三角形的面积？

Answer 1

（1）连接OC，
∵CD为切线，
∴∠DCO=90°
∵∠A=30°，OA=OC，
∴∠ACO=30°
∵AB是直径，
∴∠ACB=90°，∠OCB=60°，
∴∠BCD=30°，∠ABC=60°，
∴∠BCD=∠A=30°，∠D=30°，
∴∠A=∠D，
∴AC=CD=3

3

，即AB=6cm．

（2）如图1：当∠BNM=90°时，MN∥AC，
∴

6-3t

6

=

1.5t

3

，得t=1，即MN恰为△ACB的中位线，
∴S=

1

2

×

3

2

×

3 3

2

=

9 3

8

cm²，
当∠BMN=90°时，cos∠MBN=

BM

BN

，
即cos60°=

6-3t

1.5t

，解得t=1.6，
此时，MN=

3

BM=

3

（6-3t）=1.2

3

，
S=

1

2

×1.2

3

×1.2=

18 3

25

cm²．