题目内容
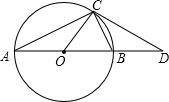
如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)若⊙O的半径为3,ED=4,EO的延长线交⊙O于F,连DF、AF,求△ADF的面积.

(1)求证:ED为⊙O的切线;
(2)若⊙O的半径为3,ED=4,EO的延长线交⊙O于F,连DF、AF,求△ADF的面积.

(1)证明:连接OD,CD,
∵AC是⊙O的直径,
∴∠CDA=90°=∠BDC,
∵OE∥AB,CO=AO,
∴BE=CE,
∴DE=CE,
∵在△ECO和△EDO中
,
∴△ECO≌△EDO,
∴∠EDO=∠ACB=90°,
即OD⊥DE,OD过圆心O,
∴ED为⊙O的切线.
(2)过O作OM⊥AB于M,过F作FN⊥AB于N,
则OM∥FN,∠OMN=90°,
∵OE∥AB,
∴四边形OMFN是矩形,
∴FN=OM,
∵DE=4,OC=3,由勾股定理得:OE=5,
∴AC=2OC=6,
∵OE∥AB,
∴△OEC∽△ABC,
∴
=
,
∴
=
,
∴AB=10,
在Rt△BCA中,由勾股定理得:BC=
=8,
sin∠BAC=
=
=
,
即
=
,
OM=
=FN,
∵cos∠BAC=
=
=
,
∴AM=
由垂径定理得:AD=2AM=
,
即△ADF的面积是
AD×FN=
×
×
=
.
答:△ADF的面积是
.

∵AC是⊙O的直径,
∴∠CDA=90°=∠BDC,
∵OE∥AB,CO=AO,
∴BE=CE,
∴DE=CE,
∵在△ECO和△EDO中
|
∴△ECO≌△EDO,
∴∠EDO=∠ACB=90°,
即OD⊥DE,OD过圆心O,
∴ED为⊙O的切线.
(2)过O作OM⊥AB于M,过F作FN⊥AB于N,
则OM∥FN,∠OMN=90°,
∵OE∥AB,
∴四边形OMFN是矩形,
∴FN=OM,

∵DE=4,OC=3,由勾股定理得:OE=5,
∴AC=2OC=6,
∵OE∥AB,
∴△OEC∽△ABC,
∴
| OC |
| AC |
| OE |
| AB |
∴
| 3 |
| 6 |
| 5 |
| AB |
∴AB=10,
在Rt△BCA中,由勾股定理得:BC=
| 102-62 |
sin∠BAC=
| BC |
| AB |
| OM |
| OA |
| 8 |
| 10 |
即
| OM |
| 3 |
| 4 |
| 5 |
OM=
| 12 |
| 5 |
∵cos∠BAC=
| AC |
| AB |
| AM |
| OA |
| 3 |
| 5 |
∴AM=
| 9 |
| 5 |
由垂径定理得:AD=2AM=
| 18 |
| 5 |
即△ADF的面积是
| 1 |
| 2 |
| 1 |
| 2 |
| 18 |
| 5 |
| 12 |
| 5 |
| 108 |
| 25 |
答:△ADF的面积是
| 108 |
| 25 |

练习册系列答案
相关题目