Question

已知：如图，AB、AC、ED分别切⊙O于点B、C、D，且AC⊥DE于E，BC的延长线交直线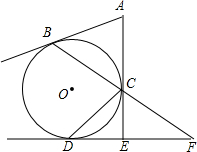DE于点F．若BC=24，sin∠F=

3

5

．
（1）求EF的长；
（2）试判断直线AB与CD是否平行？若平行，给出证明；若不平行，说明理由．

Answer 1

（1）在Rt△CEF中，∠CEF=90°，
由sin∠F=

3

5

，设CE=3x，CF=5x，
由勾股定理得EF=4x，
∵ED、EC分别切⊙O于点D、C，
∴ED=EC=3x，
由切割线定理得FD²=FC•FB，即（7x）²=5x•（5x+24），
∴x²-5x=0，
∴x₁=5，x₂=0（不合题意，舍去），
∴EF=4x=20；（4分）

（2）AB与CD不平行，（5分）
连接BD，
∵ED切⊙O于点D，
∴∠CBD=∠CDF，
又∵∠F=∠F，
∴△BDF∽△DCF，
∴

BD

DC

=

DF

CF

，
∵CF=5x=25，DF=7x=35，
在等腰直角△CDE中，可求得DC=15

2

，
∴BD=21

2

，（7分）BC=24，
∴BD≠BC，
∴∠BDC≠∠BCD，
又∵AB切⊙O于点B，
∴∠ABC=∠BDC，
∴∠ABC≠∠BCD，
∴AB与CD不平行．（8分）